科目：gzsx 来源： 题型：013
(
全国联考模拟)高三(1)、(2)、(3)、(4)、(5)班进行4×100米接力赛时，没有出现两个班同时到达终点的情况，则(2)班的名次在(3)、(4)、(5)班名次之前的所有排列情况共有[
]|
A ．36种 |
B ．30种 |
C ．27种 |
D ．24种 |
科目：gzsx 来源： 题型：
全国硕士研究生入学统一考试初试时间为每年的1月中下旬左右.在2006年，全国硕士研究生招生报考人数为127.5万，与去年同比增长9％.据专家分析，2007年的报考人数将与2006年不分上下，竞争将异常激烈.年年攀升的考研报考人数，让我们不禁好奇.考生的报考热门专业是哪些呢？最近两年的统计数据见下表：
专业名称 | 2006报考人数 | 2005报考人数 |
企业管理 | 164 200 | 153 700 |
法律硕士 | 95 500 | 174 200 |
MBA | 139 200 | 144 600 |
英语语言文学 | 126 600 | 130 900 |
金融 | 128 000 | 134 300 |
计算机应用技术 | 81 400 | 104 900 |
会计学 | 76 300 | 64 100 |
管理科学与工程 | 72 300 | 1 300 |
设计艺术学 | 72 100 | 62 200 |
你能用不同的方式分别表示各热门专业的报考情况吗？（以2006年的情形为例）.
科目：gzsx 来源： 题型：
全国篮球职业联赛的某个赛季在H队与F队之间角逐。采取七局四胜制（无平局），即若有一队胜4场，则该队获胜并且比赛结束。设比赛双方获胜是等可能的。根据已往资料显示，每场比赛的组织者可获门票收入100万元。组织者在此赛季中，两队决出胜负后，门票收入不低于500万元的概率是____________________．
科目：gzsx 来源： 题型：022
(2006
全国Ⅱ，16)一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图(如图所示)．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在[2 500，3 000)(元)月收入段应抽出__________人．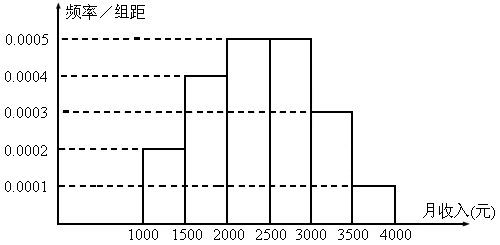
科目：gzsx 来源： 题型：
(07年全国卷Ⅱ文)（12分）
从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件
：“取出的2件产品中至多有1件是二等品”的概率
．
（1）求从该批产品中任取1件是二等品的概率
；
（2）若该批产品共100件，从中任意抽取2件，求事件
：“取出的2件产品中至少有一件二等品”的概率
．
科目：gzsx 来源： 题型：
(07年全国卷Ⅱ理)从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有2人参加，星期六、星期日各有1人参加，则不同的选派方法共有
(A)40种 (B) 60种 (C) 100种 (D) 120种
科目：gzsx 来源： 题型：
(07年全国卷Ⅱ理)（12分）从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件A：“取出的2件产品中至多有1件是二等品”的概率P（A）=0.96
(1)求从该批产品中任取1件是二等品的概率p;
（2）若该批产品共有100件，从中任意抽取2件，x表示取出的2件产品中二等品的件数，求x的分布列
科目：gzsx 来源：2016届广东省深圳市高三第二次调研考试数学（文）试卷（解析版） 题型：解答题
2016年全国两会，即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议，分别于2016年3月5日和3月3日在北京开幕．为了解哪些人更关注两会，某机构随机抽取了年龄在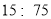
岁之间的100人进行调查，并按年龄绘制的频率分布直方图如下图所示，其分组区间为：
．把年龄落在区间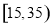
和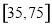
内的人分别称为“青少年人”和“中老年人”，经统计“青少年人”与“中老年人”的人数之比为9：11．
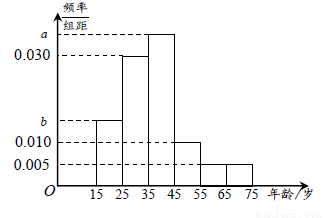
（1）求图中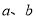
的值；
（2）若“青少年人”中有15人在关注两会，根据已知条件完成下面的
列联表，根据此统计结果能否
有99%的把握认为“中老年人”比“青少年人”更加关注两会？
关注 | 不关注 | 合计 | |
青少年人 | 15 | ||
中老年人 | |||
合计 | 50 | 50 | 100 |
附参考公式：
，其中
．
临界值表：
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
科目：gzsx 来源： 题型：
（04年全国卷IV文）（12分）
某同学参加科普知识竞赛，需回答3个问题.竞赛规则规定：答对第一、二、三问题分别得100分、100分、200分，答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6，且各题答对与否相互之间没有影响.
（Ⅰ）求这名同学得300分的概率；
（Ⅱ）求这名同学至少得300分的概率.
科目：gzsx 来源： 题型：
（04年全国卷IV理）（12分）
某同学参加科普知识竞赛，需回答三个问题.竞赛规则规定：每题回答正确得100分，回答不正确得－100分.假设这名同学每题回答正确的概率均为0.8，且各题回答正确与否相互之间没有影响.
（Ⅰ）求这名同学回答这三个问题的总得分
的概率分布和数学期望；
（Ⅱ）求这名同学总得分不为负分（即≥0）的概率.
科目：gzsx 来源：2015数学一轮复习迎战高考：5-4数列求和（解析版） 题型：选择题
[2012·大纲全国卷]已知等差数列{an}的前n项和为Sn，a5＝5，S5＝15，则数列
的前100项和为( )
A.
B.
C.
D.
科目：gzsx 来源：2012年河北省保定市高考数学一模试卷（理科）（解析版） 题型：解答题
科目：gzsx 来源： 题型：
科目：gzsx 来源： 题型：
十二届全国人大二次会议上，李克强总理提出“以雾霾频发的特大城市和区域为重点，以细颗粒物PM2.5和可吸入颗粒物PM10为突破口…”治理污染，“要像对贫困宣战一样，坚决向污染宣战”，其中总理提到的“PM2.5”是指大气中直径小于或等于2.5微米的颗粒物，也称为人肺颗粒物．根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米-75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．从某市2013年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本，监测值频数如茎叶图所示（十位为茎，个位为叶）：科目：gzsx 来源： 题型：解答题
| 课程 人数 班级 | 选修4-1 | 选修4-4 | 选修4-5 |
| A | 10 | a | 15 |
| B | 10 | 20 | b |
科目：gzsx 来源： 题型：解答题
为备战“全国高中数学联赛”，我市某高中拟成立两个“数学竞赛班”，经过学校预选，选出40名学生，编成A，B两个班，分别由两位教师担任教练进行培训；经过两个月的培训，参加了市里组织的数学竞赛初赛（只有经过初赛，取得相应名次，才能取得参加省统一组织的“全国高中数学联赛”复赛资格），这40名学生的初赛成绩的茎叶图如图：| A班 | B班 | 合计 | |
| 种子选手 | |||
| 非种子选手 | |||
| 合计 |
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
中，
，则前10项的和
＝( )
的前100项和为( )
的前100项和为( )
