
科目:gzsx 来源: 题型:
| AB |
| AC |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
| A、等腰非等边三角形 |
| B、等边三角形 |
| C、三边均不相等的三角形 |
| D、直角三角形 |
科目:gzsx 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练19练习卷(解析版) 题型:解答题
已知△ABC的三边长|AB|= ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ +μ
+μ ,且λμ=
,且λμ= .
.

(1)求| |最小值,并指出此时
|最小值,并指出此时 与
与 ,
, 的夹角;
的夹角;
(2)是否存在两定点F1,F2使|| |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
科目:gzsx 来源: 题型:解答题
已知△ABC的三边长|AB|=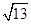 ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ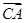 +μ
+μ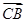 ,且λμ=
,且λμ=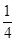 .
.
(1)求| |最小值,并指出此时
|最小值,并指出此时 与
与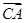 ,
,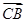 的夹角;
的夹角;
(2)是否存在两定点F1,F2使||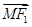 |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
科目:gzsx 来源:不详 题型:单选题
| AB |
| AC |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
| A.等边三角形 | B.直角三角形 |
| C.等腰非等边三角形 | D.三边均不相等的三角形 |
科目:gzsx 来源:陕西 题型:单选题
| AB |
| AC |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
| A.等腰非等边三角形 | B.等边三角形 |
| C.三边均不相等的三角形 | D.直角三角形 |
科目:gzsx 来源:不详 题型:解答题
 ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ +μ
+μ ,且λμ=
,且λμ= .
.
 |最小值,并指出此时
|最小值,并指出此时 与
与 ,
, 的夹角;
的夹角; |-|
|-| ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.科目:gzsx 来源: 题型:
已知△ABC的三边长|AB|= ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足 =λ
=λ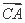 +μ
+μ ,且λμ=
,且λμ= .
.

(1)求| |最小值,并指出此时
|最小值,并指出此时 与
与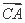 ,
, 的夹角;
的夹角;
(2)是否存在两定点F1,F2使|| |-|
|-|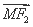 ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
科目:czsx 来源:广东省期末题 题型:解答题

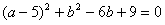 ,求BF的长;
,求BF的长;科目:czsx 来源:期末题 题型:解答题
 ,求BF的长;
,求BF的长;
科目:czsx 来源: 题型:
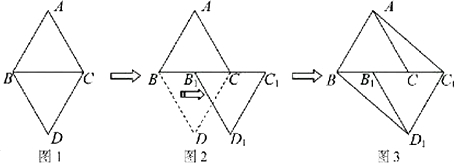
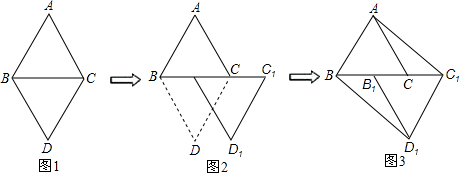
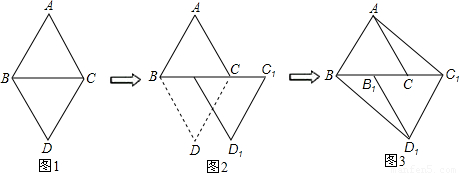
如图①,已知等边△ABC和等边△DBC有公共的底边BC
(1)以图①中的某个点为旋转中心,旋转△ABC和△DBC重合则旋转中心为________(写出所有满足条件的点);
(2)如图②,已知![]() 是线段BC的中点,现沿着由B到
是线段BC的中点,现沿着由B到![]() 的方向,将△DBC平移到
的方向,将△DBC平移到![]() 的位置,连结
的位置,连结![]() ,
,![]() ,得到四边形
,得到四边形![]() 是什么特殊的四边形?说明你的理由.
是什么特殊的四边形?说明你的理由.
(3)在四边形![]() 中有_________对全等三角形?请你选出其中一对进行证明.
中有_________对全等三角形?请你选出其中一对进行证明.

科目:czsx 来源: 题型:
 如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.
如图,已知△ABC是等边三角形,D为AC上一个动点,延长AB至E,使BE=CD,连接DE交BC于点F.科目:czsx 来源: 题型:
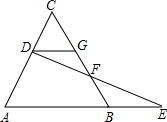 如图,已知△ABC是等边三角形,D为AC边上的一点,DG∥AB,延长AB到E,使BE=GD,连接DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一点,DG∥AB,延长AB到E,使BE=GD,连接DE交BC于F.科目:czsx 来源: 题型:
 如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,DG∥AB,延长AB到E,使BE=CD,连结DE交BC于F.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
科目:czsx 来源:天门模拟 题型:解答题

科目:czsx 来源:2006年湖北省天门市九年级数学联考试卷(解析版) 题型:解答题
科目:gzsx 来源:2010-2011学年北京大学附中高三(上)数学练习试卷4(文科)(解析版) 题型:填空题
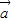 与
与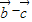 都是非零向量,则“
都是非零向量,则“ ”是“
”是“ ”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是
”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是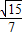 ;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设
;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设 ,
,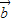 ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足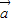 与
与 不共线,
不共线, ⊥
⊥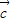 ,|
,| |=|
|=|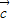 |,则|
|,则| •
•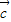 |的值一定等于以
|的值一定等于以 ,
,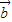 为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)
为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)