
科目:czsx 来源: 题型:
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于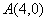 ,与y轴交于
,与y轴交于 ,点C为劣弧
,点C为劣弧 的中点,连接AC并延长到D,使
的中点,连接AC并延长到D,使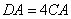 ,连接BD.
,连接BD.
(1) 求⊙M的半径;
求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使 最大.
最大.
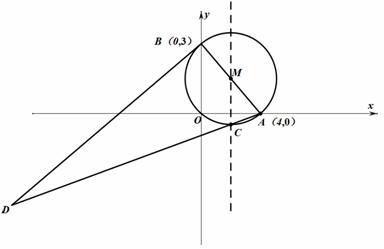
科目:czsx 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.

科目:czsx 来源: 题型:
 如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.科目:czsx 来源: 题型:
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.

科目:czsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:解答题
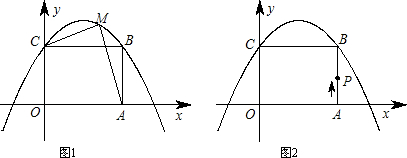
 x2+bx+c经过B,C两点.
x2+bx+c经过B,C两点. x2+bx+c上一点,连接AM,MC,设四边形OAMC的面积为S,求S关于x的函数关系式,并回答:x为何值时S取得最大值?
x2+bx+c上一点,连接AM,MC,设四边形OAMC的面积为S,求S关于x的函数关系式,并回答:x为何值时S取得最大值? x2+bx+c上找到点D,使得以P,D,C为顶点的三角形是等腰直角三角形?如果能,请求出D点坐标;如果不能,请说明理由.
x2+bx+c上找到点D,使得以P,D,C为顶点的三角形是等腰直角三角形?如果能,请求出D点坐标;如果不能,请说明理由.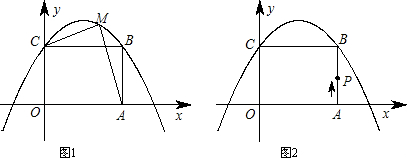
科目:czsx 来源:2010年浙江省金华市武义县中考数学模拟试卷(解析版) 题型:解答题
 x2+bx+c经过B,C两点.
x2+bx+c经过B,C两点. x2+bx+c上一点,连接AM,MC,设四边形OAMC的面积为S,求S关于x的函数关系式,并回答:x为何值时S取得最大值?
x2+bx+c上一点,连接AM,MC,设四边形OAMC的面积为S,求S关于x的函数关系式,并回答:x为何值时S取得最大值? x2+bx+c上找到点D,使得以P,D,C为顶点的三角形是等腰直角三角形?如果能,请求出D点坐标;如果不能,请说明理由.
x2+bx+c上找到点D,使得以P,D,C为顶点的三角形是等腰直角三角形?如果能,请求出D点坐标;如果不能,请说明理由.
科目:czsx 来源:2009年浙江省杭州市萧山区中考模拟数学试卷(宁围镇中 洪卫)(解析版) 题型:解答题

科目:czsx 来源: 题型:
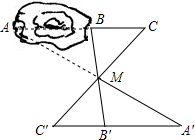 如图,为了测量湖宽AB,先在AB的延长线上选定点C,再选一适当的点M,然后延长BM,CM到B′,C′,使MB′=MB,MC′=MC.又在C′B′的延长线上找一点A′,使A′,M,A三点在同一直线上,这时,只要测出线段A′B′的长度就可知湖宽,你能说明其中的道理吗?
如图,为了测量湖宽AB,先在AB的延长线上选定点C,再选一适当的点M,然后延长BM,CM到B′,C′,使MB′=MB,MC′=MC.又在C′B′的延长线上找一点A′,使A′,M,A三点在同一直线上,这时,只要测出线段A′B′的长度就可知湖宽,你能说明其中的道理吗?科目:czsx 来源: 题型:解答题
如图,已知抛物线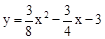 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.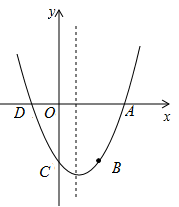
科目:czsx 来源:不详 题型:解答题
 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
科目:czsx 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.

科目:czsx 来源: 题型:
如图8,已知抛物线y= 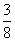 x2-
x2- 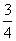 x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C。
x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C。
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由。
科目:czsx 来源:2016届山东济南天桥区九年级第一次模拟考试数学试卷(解析版) 题型:解答题
如图,已知直线y=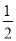 x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y=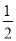 x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标;
(3)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.

科目:czsx 来源:2016-2017学年吉林长春八中等三校联考九年级上10月考数学卷(解析版) 题型:解答题
如图,已知直线y=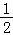 x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x+1与y轴交于点A,与x轴交于点D,抛物线y=x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标;
(3)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.

科目:czsx 来源:2009年四川省眉山市中考数学试题及答案(纯word版) 题型:044
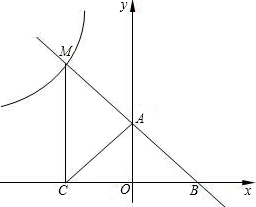
已知:直线![]() 与y轴交于A,与x轴交于D,抛物线
与y轴交于A,与x轴交于D,抛物线![]() 与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).![]()

(1)求抛物线的解析式;
(2)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.
(3)在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标.
科目:czsx 来源: 题型:
如图,已知直线 与y轴交于点A,与x轴交于点D,抛物线
与y轴交于点A,与x轴交于点D,抛物线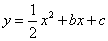 与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0)。
与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0)。
⑴求该抛物线的解析式;
⑵动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标。
⑶在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标。
