
科目:czsx 来源: 题型:解答题
 已知:关于x的一元二次方程x2-(1+2k)x+k2-2=0有两个实数根.
已知:关于x的一元二次方程x2-(1+2k)x+k2-2=0有两个实数根.科目:czsx 来源:2012年北京市门头沟区中考数学一模试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
 (2012•门头沟区一模)已知:关于x的一元二次方程x2-(1+2k)x+k2-2=0有两个实数根.
(2012•门头沟区一模)已知:关于x的一元二次方程x2-(1+2k)x+k2-2=0有两个实数根.科目:czsx 来源: 题型:
 已知抛物线y=
已知抛物线y=| 1 |
| 2 |
| 3 |
| 2 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
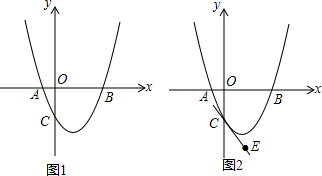 已知抛物线y=
已知抛物线y= mx2-
mx2- mx-2m交x轴于A(x1,0),B(x2,0)交y轴负半轴于C点,且x1<0<x2,(AO+OB)2=12CO+1.
mx-2m交x轴于A(x1,0),B(x2,0)交y轴负半轴于C点,且x1<0<x2,(AO+OB)2=12CO+1.科目:czsx 来源: 题型:解答题
科目:czsx 来源:不详 题型:解答题
| 1 |
| 2 |
| 3 |
| 2 |

科目:czsx 来源: 题型:解答题
科目:czsx 来源:不详 题型:解答题
科目:czsx 来源: 题型:
已知关于x的一元二次方程kx2+(3k+1)x+2k+1=0.
(1)求证:该方程必有两个![]() 实数根.
实数根.
(2)若该方程只有整数根,求k的整数值
(3)在(2)的条件下,在平面直角坐标系中,若二次函数y=(k+1)x2+3x+m与x轴有两个不同的交点A和B(A在B左侧),并且满足OA=2·OB,求m的非负整数值.
科目:czsx 来源: 题型:
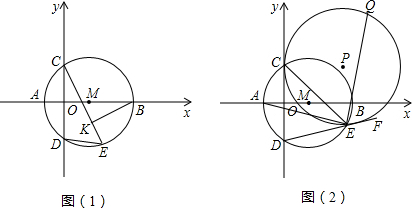
| 1 |
| 2 |
| EC+ED |
| EA |
| 3 |
| EC+EF |
| EQ |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
 已知:二次函数y=x2-mx+
已知:二次函数y=x2-mx+| 3 |
| 4 |
| 3 |
| 4 |
科目:gzsx 来源: 题型:
|
|
| π |
| 4 |
3
| ||
| 2 |
| a2 |
| b |
| b2 |
| a |
| (1-x)2 |
| x |
| x2 |
| 1-x |
科目:gzsx 来源: 题型:
|
|
| π |
| 2 |
|
| x-3 |
| 5-x |
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:解答题
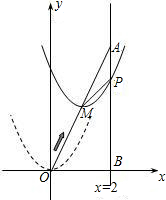 (1)已知二次函数y=ax2+bx+c(a≠0)的图象开口向下,并经过点(-1,2),(1,0).下列命题其中一定正确的是______.
(1)已知二次函数y=ax2+bx+c(a≠0)的图象开口向下,并经过点(-1,2),(1,0).下列命题其中一定正确的是______.科目:czsx 来源:2009-2010学年九年级(上)数学期末检测模拟试卷(三)(解析版) 题型:解答题
科目:czsx 来源:2008-2009学年浙江省湖州市白雀学校九年级(上)期中数学试卷(解析版) 题型:解答题
