
科目:czsx 来源: 题型:
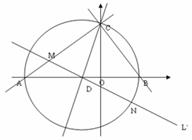
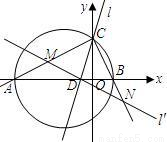
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C
若C的坐标为(0,2),AB=5, A,B两点的横坐标XA,XB是关于X的方程![]() 的两根:
的两根:
(1) 求m,n的值
(2) 若∠ACB的平分线所在的直线![]() 交x轴于点D,试求直线
交x轴于点D,试求直线![]() 对应的一次函数的解析式
对应的一次函数的解析式
科目:czsx 来源: 题型:
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C,若C的坐标为(0,2),AB=5,A,B两点的横坐标XA,XB是关于X的方程的两根:
1.求m,n的值;
2.若∠ACB的平分线所在的直线交x轴于点D,试求直线
对应的一次函数的解析式;
3.过点D任作一直线分别交射线CA,CB(点C除外)于点M,N,则
的值是否为定值,若是,求出定值,若不是,请说明理由
科目:czsx 来源: 题型:
 的两根:
的两根:
 交x轴于点D,试求直线
交x轴于点D,试求直线 对应的一次函数的解析式;
对应的一次函数的解析式; 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则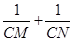 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由 科目:czsx 来源:2010-2011学年福建莆田秀屿区实验中学中考模拟数学试卷 题型:解答题
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C,若C的坐标为(0,2),AB=5,
A,B两点的横坐标XA,XB是关于X的方程 的两根:
的两根:

1.求m,n的值;
2.若∠ACB的平分线所在的直线 交x轴于点D,试求直线
交x轴于点D,试求直线 对应的一次函数的解析式;
对应的一次函数的解析式;
3.过点D任作一直线 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由
科目:czsx 来源:不详 题型:解答题
 的两根:
的两根:
 交x轴于点D,试求直线
交x轴于点D,试求直线 对应的一次函数的解析式;
对应的一次函数的解析式; 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由科目:czsx 来源: 题型:
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的 过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
(1)求点A、B的坐标及抛物线的解析式。
(2)若∠ACB的平分线所在的直线 交x轴于点D,交圆于点E。
交x轴于点D,交圆于点E。
①求证:PE⊥x轴;
②试求直线 对应的一次函数的解析式.
对应的一次函数的解析式.
(3)过点D任作一直线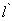 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由
 |
科目:gzsx 来源: 题型:选择题
| A. | $[\frac{2}{3},\frac{4}{3}]$ | B. | $[\frac{1}{3},\frac{2}{3}]$ | C. | [0,2] | D. | $[0,\frac{{2\sqrt{5}}}{3}]$ |
科目:czsx 来源:2016届江苏省无锡市南长区九年级上学期期中考试数学试卷(解析版) 题型:解答题
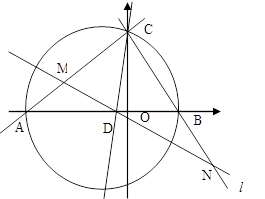
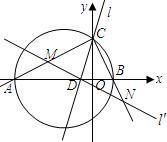
在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.
(1)求点C的坐标;
(2)若∠ACB的平分线所在的直线l交x轴于点D,求直线l对应的一次函数关系式;
(3)过点D任作一直线l′分别交射线CA、CB(点C除外)于点M、N,则 +
+ 的值是否为定值?若是,求出定值;若不是,请说明理由.
的值是否为定值?若是,求出定值;若不是,请说明理由.
科目:czsx 来源: 题型:解答题
 在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.
在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.科目:czsx 来源: 题型:
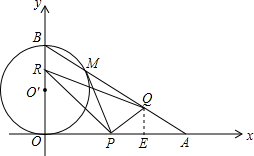 如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=12
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=12| 3 |
| 3 |
科目:czsx 来源: 题型:
 标为(0,2),AB=5,A,B两点的横坐标xA,xB是关于x的方程x2-(m+2)x+n-1=0的两根.
标为(0,2),AB=5,A,B两点的横坐标xA,xB是关于x的方程x2-(m+2)x+n-1=0的两根.| 1 |
| CM |
| 1 |
| CN |
科目:czsx 来源: 题型:
| 3 |
| 3 |
科目:czsx 来源:江苏省无锡市天一实验学校2012届九年级一模数学试题 题型:044
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=12![]() cm,点B在y轴的正半轴上,OB=12 cm,动点P从点O开始沿OA以2
cm,点B在y轴的正半轴上,OB=12 cm,动点P从点O开始沿OA以2![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4 cm/s的速度向点B移动,动点R从点B开始沿BO以2 cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4 cm/s的速度向点B移动,动点R从点B开始沿BO以2 cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
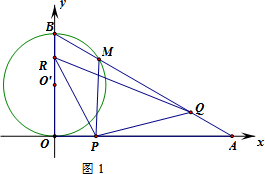
(1)求∠OAB的度数.
(2)以OB为直径的⊙O′与AB交于点M,当t为何值时,PM与⊙O′相切?
(3)是否存在△RPQ为等腰三角形?若存在,请直接写出t值;若不存在,请说明理由.
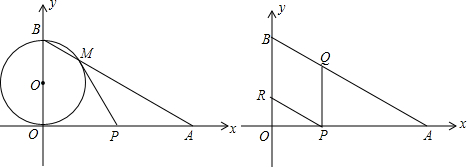
科目:czsx 来源:江苏省泰州中学附属初中2012届九年级下学期期中考试数学试题 题型:044
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=12![]() cm,点B在y轴的正半轴上,OB=12 cm,动点P从点A开始沿AO以
cm,点B在y轴的正半轴上,OB=12 cm,动点P从点A开始沿AO以![]() cm/s的速度向点O移动,移动时间为t s(0<t<6).
cm/s的速度向点O移动,移动时间为t s(0<t<6).
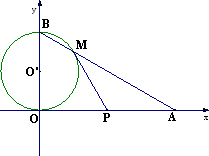

(1)求∠OAB的度数.
(2)以OB为直径的⊙![]() 与AB交于点M,当t为何值时,PM与⊙
与AB交于点M,当t为何值时,PM与⊙![]() 相切?
相切?
(3)动点Q从点A开始沿AB以4 cm/s的速度向点B移动,动点R从点B开始沿BO以2 cm/s的速度向点O移动.如果P、Q、R分别从A、A、B同时移动,当t=4 s时,试说明四边形BRPQ为菱形;
(4)在(3)的条件下,以R为圆心,r为半径作⊙R,当r不断变化时,⊙R与菱形BRPQ各边的交点个数将发生变化,随当交点个数发生变化时,请直接写出r的对应值或取值范围.
科目:czsx 来源:云南省红河哈尼族彝族自治州2010年高中(中专)招生统一考试数学试卷 题型:044
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=![]() cm,点B在y轴的正半轴上,OB=12 cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12 cm,动点P从点O开始沿OA以![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4 cm/s的速度向点B移动,动点R从点B开始沿BO以2 cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4 cm/s的速度向点B移动,动点R从点B开始沿BO以2 cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
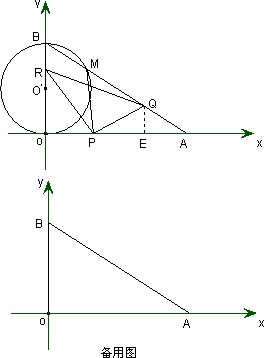
(1)求∠OAB的度数.
(2)以OB为直径的⊙![]() 与AB交于点M,当t为何值时,PM与⊙
与AB交于点M,当t为何值时,PM与⊙![]() 相切?
相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t值.
(4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.
科目:czsx 来源: 题型:解答题
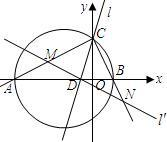 标为(0,2),AB=5,A,B两点的横坐标xA,xB是关于x的方程x2-(m+2)x+n-1=0的两根.
标为(0,2),AB=5,A,B两点的横坐标xA,xB是关于x的方程x2-(m+2)x+n-1=0的两根.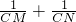 的是否为定值?若是,求出该定值;若不是,请说明理由.
的是否为定值?若是,求出该定值;若不是,请说明理由.科目:czsx 来源:四川省中考真题 题型:解答题

 的是否为定值?若是,求出该定值;若不是,请说明理由。
的是否为定值?若是,求出该定值;若不是,请说明理由。科目:czsx 来源:2012届江苏省泰州中学附属初级中学九年级下学期期中考试数学卷(带解析) 题型:解答题
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=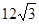 cm,点B在y轴的正半轴上,OB=12cm,动点P从点A开始沿AO以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点A开始沿AO以 cm/s的速度向点O移动,移动时间为t s(0<t<6).
cm/s的速度向点O移动,移动时间为t s(0<t<6).
(1)求∠OAB的度数. (2分)
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时, PM与⊙O‘相切?
(3分)(3)动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动. 如果P、Q、R分别从A、A、B同时移动,当t="4" s时,试说明四边形BRPQ为菱形;(3分)
(4)在(3)的条件下,以R为圆心,r为半径作⊙R,当r不断变化时,⊙R与菱形BRPQ各边的交点个数将发生变化,随当交点个数发生变化时,请直接写出r的对应值或取值范围.(4分)
科目:czsx 来源:2011年福建省莆田市秀屿区实验中学中考数学模拟试卷(解析版) 题型:解答题
 的是否为定值?若是,求出该定值;若不是,请说明理由.
的是否为定值?若是,求出该定值;若不是,请说明理由.
科目:czsx 来源:2011-2012学年江苏省附属初级中学九年级下学期期中考试数学卷(解析版) 题型:解答题
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=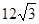 cm,点B在y轴的正半轴上,OB=12cm,动点P从点A开始沿AO以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点A开始沿AO以 cm/s的速度向点O移动,移动时间为t
s(0<t<6).
cm/s的速度向点O移动,移动时间为t
s(0<t<6).

(1)求∠OAB的度数. (2分)
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时, PM与⊙O‘相切?
(3分)(3)动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动. 如果P、Q、R分别从A、A、B同时移动,当t=4 s时,试说明四边形BRPQ为菱形;(3分)
(4)在(3)的条件下,以R为圆心,r为半径作⊙R,当r不断变化时,⊙R与菱形BRPQ各边的交点个数将发生变化,随当交点个数发生变化时,请直接写出r的对应值或取值范围.(4分)