16 若.则 A.1 B.2 C.3 D.4 下一题答案解析
科目:gzsx
来源:
题型:
下列命题
①命题“若am
2>bm
2,则a>b”的逆命题是真命题;
②若
=(4,3),
=(-2,1),则
在
上的投影是
-;
③在(
+
)
16的二项展开式中,有理项共有4项;
④已知一组正数x
1,x
2,x
3,x
4的方差为
s2=(x12+x22+x32+x42-16),则数据x
1+2,x
2+2,x
3+2,x
4+2的平均数为4;
⑤复数
的共轭复数是a+bi(a,b∈R),则ab=-6.
其中真命题的个数为( )
查看答案和解析>>
科目:gzsx
来源:2012年上海市财大附中高三4月检测数学试卷(解析版)
题型:选择题
下列命题
①命题“若am
2>bm
2,则a>b”的逆命题是真命题;
②若

,

,则

在

上的投影是

;
③在(

+

)
16的二项展开式中,有理项共有4项;
④已知一组正数x
1,x
2,x
3,x
4的方差为

,则数据x
1+2,x
2+2,x
3+2,x
4+2的平均数为4;
⑤复数

的共轭复数是a+bi(a,b∈R),则ab=-6.
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:gzsx
来源:
题型:选择题
16.给出下列命题:
①若{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}可以作为空间的一个基底,$\overrightarrow{d}$与$\overrightarrow{c}$共线,$\overrightarrow{d}$≠0,则{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{d}$}也可作为空间的一个基底;
②已知向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$,$\overrightarrow{b}$与任何向量都不能构成空间的一个基底;
③A,B,M,N是空间四点,若$\overrightarrow{BA}$,$\overrightarrow{BM}$,$\overrightarrow{BN}$不能构成空间的一个基底,那么A,B,M,N共面;
④已知向量组{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}是空间的一个基底,若$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{c}$,则{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{m}$}也是空间的一个基底.
其中正确命题的个数是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
下列命题错误的是( )
| A、命题“若lgx=0,则x=1”的逆否命题为“若x≠1,则lgx≠0” |
| B、命题“若x>2,则<”的否命题是“若x>2,则≥” |
| C、双曲线-=1的渐近线方程为y=±x |
| D、若p∧q为假命题,则p与q中至少有一个为假命题 |
查看答案和解析>>
科目:gzsx
来源:
题型:
给出下列命题
①△ABC中,sinA=
,cosB=
,则cosC=-
;
②角α终边上一点P(-3a,4a),且a≠0,那么cosα=-
;
③若函数f(x)=3sin(ωx+φ)对于任意的x都有f(
+x)=-f(
-x),则f(
)=0;
④已知f(x)=sin(ωx+2)满足f(x+2)+f(x)=0,则ω=
;
其中正确的个数有( )
查看答案和解析>>
科目:gzsx
来源:
题型:013
(2006
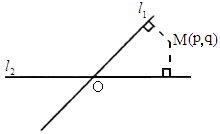
上海,16)如图所示,平面中两条直线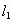 和
和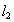 相交于点O,对于平面上任意一点M,若p、q分别是M到直线
相交于点O,对于平面上任意一点M,若p、q分别是M到直线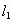 和
和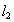 的距离,则称有序非负数实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0给出下列三个命题;
的距离,则称有序非负数实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0给出下列三个命题;
①若
p=q=0,则“距离坐标”为(0,0)的点有且仅有1个.
②若
pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个.
③若
pq≠0,则“距离坐标”为(p,q)的点有且仅有4个.
上述命题中,正确命题的个数是
[
]
查看答案和解析>>
科目:gzsx
来源:2013届浙江省宁波市高一下期末考数学试卷
题型:选择题
把正整数按一定的规则排成了如图所示的三角形数表.设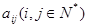 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第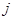 个数,如
个数,如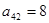 ,
,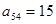 .若
.若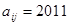 ,则
,则 与
与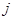 的和为
的和为
A. 106 B.107 C.108 D.109
1
2
4
3
5 7
6
8 10 12
9
11 13 15 17
14 16 18 20
22 24
……………………………………
(第10题图)
查看答案和解析>>
科目:gzsx
来源:
题型:
把正整数按一定的规则排成了如图所示的三角形数表.设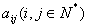 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第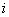 行、从左往右数第
行、从左往右数第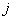 个数,如
个数,如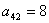 ,
,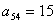 .若
.若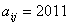 ,则
,则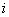 与
与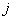 的和为
的和为
A. 106 B.107 C.108 D.109
1
2 4
3 5 7
6 8 10 12
9 11 13 15 17
14 16 18 20 22 24
……………………………………
(第10题图)
查看答案和解析>>
科目:gzsx
来源:
题型:
在莫言获得诺贝尔奖后,某高校在男、女生中各抽取50名,调查对莫言作品的了解程度,统计结果如下表所示:
| 阅读过莫言作品的作品是(篇) |
[0,25) |
[25,50) |
[50,75) |
[75,100) |
[100,125) |
| 男生人数 |
6 |
12 |
18 |
10 |
4 |
| 女生人数 |
4 |
16 |
16 |
13 |
1 |
(Ⅰ)试估计该校学生阅读莫言作品不低于50篇的概率;
(Ⅱ)若对莫言作品阅读低于50篇称为对莫言作品“一般了解”,否则称为对莫言作品“非常了解”,根据题意完成下表,并判断对莫言作品的了解程度是否与性别有关.
参考数据及公式如下:
| P(K2≥k) |
0.05 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
K
2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
.
查看答案和解析>>
科目:gzsx
来源:
题型:
下列四个判断:
①10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
②命题“若α>β,则tanα>tanβ”的逆命题为真命题;
③已知a>0,b>0,则由
y=(a+b)(+)≥2•2⇒ymin=8;
④若命题“∃x∈R,|x-a|+|x+1|≤2”是假命题,则命题“∃x∈R,|x-a|+|x+1|>2”是真命题;
⑤设随机变量ξ~N(0,σ
2),且P(ξ<-1)=
,则P(0<ξ<1)=
.
其中正确的个数有( )
查看答案和解析>>
科目:gzsx
来源:2012-2013学年湖北省襄阳五中、夷陵中学、钟祥一中高三(上)11月联考数学试卷(理科)(解析版)
题型:选择题
下列四个判断:
①10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
②命题“若α>β,则tanα>tanβ”的逆命题为真命题;
③已知a>0,b>0,则由

;
④若命题“∃x∈R,|x-a|+|x+1|≤2”是假命题,则命题“∃x∈R,|x-a|+|x+1|>2”是真命题;
⑤设随机变量ξ~N(0,σ
2),且P(ξ<-1)=

,则P(0<ξ<1)=

.
其中正确的个数有( )
A.1个
B.2 个
C.3 个
D.4个
查看答案和解析>>
科目:gzsx
来源:2012-2013学年湖北省襄阳五中、夷陵中学、钟祥一中高三(上)11月联考数学试卷(理科)(解析版)
题型:选择题
下列四个判断:
①10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
②命题“若α>β,则tanα>tanβ”的逆命题为真命题;
③已知a>0,b>0,则由

;
④若命题“∃x∈R,|x-a|+|x+1|≤2”是假命题,则命题“∃x∈R,|x-a|+|x+1|>2”是真命题;
⑤设随机变量ξ~N(0,σ
2),且P(ξ<-1)=

,则P(0<ξ<1)=

.
其中正确的个数有( )
A.1个
B.2 个
C.3 个
D.4个
查看答案和解析>>
科目:gzsx
来源:
题型:
下列四个判断:
①10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
②命题“若α>β,则tanα>tanβ”的逆命题为真命题;
③已知a>0,b>0,则由y=(a+b)(
+
)≥2
•2
⇒y
min=8;
④若命题“∃x∈R,|x-a|+|x+1|≤2”是假命题,则命题“∃x∈R,|x-a|+|x+1|>2”是真命题.
其中正确的个数有( )
查看答案和解析>>
科目:gzsx
来源:
题型:填空题
下面命题:
①函数f(x)=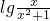 的定义域是(0,+∞);
的定义域是(0,+∞);
②在空间中,若四点不共面,则每三个点一定不共线;
③若数列{an}为等比数列,则“a3a5=16”是“a4=4”的充分不必要条件;
④直线l1经过点(3,a),B(a-2,3),直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,则a=0;
其中真命题的序号为________(写出所有真命题的序号).
查看答案和解析>>
科目:gzsx
来源:2012年安徽省马鞍山市高考数学二模试卷(文科)(解析版)
题型:解答题
下面命题:
①函数f(x)=
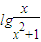
的定义域是(0,+∞);
②在空间中,若四点不共面,则每三个点一定不共线;
③若数列{a
n}为等比数列,则“a
3a
5=16”是“a
4=4”的充分不必要条件;
④直线l
1经过点(3,a),B(a-2,3),直线l
2经过点C(2,3),D(-1,a-2),若l
1⊥l
2,则a=0;
其中真命题的序号为
(写出所有真命题的序号).
查看答案和解析>>
科目:gzsx
来源:
题型:
(2012•马鞍山二模)下面命题:
①函数f(x)=
lg的定义域是(0,+∞);
②在空间中,若四点不共面,则每三个点一定不共线;
③若数列{a
n}为等比数列,则“a
3a
5=16”是“a
4=4”的充分不必要条件;
④直线l
1经过点(3,a),B(a-2,3),直线l
2经过点C(2,3),D(-1,a-2),若l
1⊥l
2,则a=0;
其中真命题的序号为
①②
①②
(写出所有真命题的序号).
查看答案和解析>>
科目:gzsx
来源:
题型:选择题
15.下列命题正确的是( )
| A. | 命题“∃x0∈R,x02-x0>0”的否定是“∀x0∈R,x02-x0<0” |
| B. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
| C. | 在回归直线$\widehat{y}$=-0.5x+3中,当解释变量x每增加一个单位时,预报变量$\widehat{y}$平均减少0.5个单位 |
| D. | 若a,b∈[0,2],则不等式a2+b2<$\frac{1}{4}$成立的概率是$\frac{π}{16}$ |
查看答案和解析>>
科目:gzsx
来源:
题型:
16.如图,平面中两条直线

和
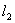
相交于点O,对于平面上任意一点M,若
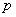
、

分别是M到直线

和

的距离,则称有序非负实数对(

,

)是点M的“距离坐标”.已知常数

≥0,
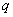
≥0,给出下列三个命题:

①若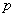 =
= =0,则“距离坐标”为(0,0)的点有且仅有1个;
=0,则“距离坐标”为(0,0)的点有且仅有1个;
②若 =0,且
=0,且 +
+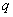 ≠0,则“距离坐标”为(
≠0,则“距离坐标”为( ,
, )的点有且仅有2个;
)的点有且仅有2个;
③若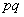 ≠0,则“距离坐标”为(
≠0,则“距离坐标”为( ,
, )的点有且仅有4个.
)的点有且仅有4个.
上述命题中,正确命题的个数是 [答]( )
(A)0;(B)1; (C)2; (D)3.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
9.某班级举办知识竞赛活动,现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:为每位参加决赛的选手准备4道判断题,选手对其依次口答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对1道,则获得二等奖.某同学进入决赛,每道题答对的概率p的值恰好与频率分布表中不少于80分的频率的值相同.
(1)求该同学恰好答满4道题而获得一等奖的概率;
(2)设该同学答题个数为X,求X的分布列及X的数学期望.
| 序号 | 分组(分数段) | 频数(人数) | 频率 |
| 1 | [60,70) | 8 | 0.16 |
| 2 | [70,80) | 22 | a |
| 3 | [80,90) | 14 | 0.28 |
| 4 | [90,100) | b | c |
| 合计 | d | 1 |
查看答案和解析>>
科目:gzsx
来源:广东省模拟题
题型:解答题
| 某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示: |
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 | 若单科成绩85分以上(含85分),则该科成绩为优秀。 |
| (1)根据上表完成下面的2×2列联表(单位:人): |
|
|
数学成绩优秀 |
数学成绩不优秀 |
合计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
|
|
|
合计 |
|
|
20 | (2)根据题(1)中表格的数据计算,有多大的把握认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率。 |
参考数据:
①假设有两个分类变量X和Y它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联 表)为: |
|
|
y1 |
y2 |
合计 |
|
x1 |
a |
b |
a+b |
|
x2 |
c |
d |
c+d |
|
合计 |
a+c |
b+d |
a+b+c+d | 则随机变量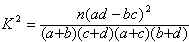 ,其中n=a+b+c+d为样本容量; ,其中n=a+b+c+d为样本容量;
②独立在检验随机变量K2的临界值参考表: |
|
|
查看答案和解析>>

 ,
, ,则
,则 在
在 上的投影是
上的投影是 ;
; +
+ )16的二项展开式中,有理项共有4项;
)16的二项展开式中,有理项共有4项; ,则数据x1+2,x2+2,x3+2,x4+2的平均数为4;
,则数据x1+2,x2+2,x3+2,x4+2的平均数为4; 的共轭复数是a+bi(a,b∈R),则ab=-6.
的共轭复数是a+bi(a,b∈R),则ab=-6.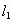 和
和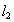 相交于点O,对于平面上任意一点M,若p、q分别是M到直线
相交于点O,对于平面上任意一点M,若p、q分别是M到直线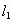 和
和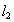 的距离,则称有序非负数实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0给出下列三个命题;
的距离,则称有序非负数实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0给出下列三个命题;

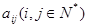 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第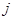 个数,如
个数,如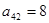 ,
,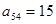 .若
.若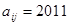 ,则
,则 与
与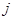 的和为
的和为
![]() 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第![]() 行、从左往右数第
行、从左往右数第![]() 个数,如
个数,如![]() ,
,![]() .若
.若![]() ,则
,则![]() 与
与![]() 的和为
的和为  ;
; ,则P(0<ξ<1)=
,则P(0<ξ<1)= .
. ;
; ,则P(0<ξ<1)=
,则P(0<ξ<1)= .
.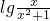 的定义域是(0,+∞);
的定义域是(0,+∞);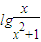 的定义域是(0,+∞);
的定义域是(0,+∞);
![]() =
=![]() =0,则“距离坐标”为(0,0)的点有且仅有1个;
=0,则“距离坐标”为(0,0)的点有且仅有1个;![]() =0,且
=0,且![]() +
+![]() ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(![]() ,
,![]() )的点有且仅有2个;
)的点有且仅有2个;![]() ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(![]() ,
,![]() )的点有且仅有4个.
)的点有且仅有4个.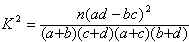 ,其中n=a+b+c+d为样本容量;
,其中n=a+b+c+d为样本容量; 