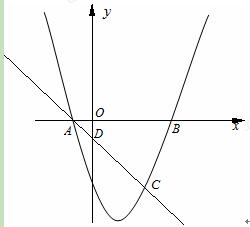
科目:czsx 来源: 题型:
如图,抛物线![]() (
(![]() )交
)交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 点坐标为(3,0),与
点坐标为(3,0),与![]() 轴交于点
轴交于点![]() (0,4),以
(0,4),以![]() 、
、![]() 为边作矩形
为边作矩形![]() 交抛物线于点
交抛物线于点![]() 。
。
(1)求抛物线的解析式;
(2)抛物线的对称轴![]() 在边
在边![]() (不包括
(不包括![]() 、
、![]() 两点)上平行移动,分别交
两点)上平行移动,分别交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,若点
,若点![]() 的横坐标为
的横坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长。
的长。
 (3)在(2)的条件下,连结
(3)在(2)的条件下,连结![]() ,则在
,则在![]() 上方的抛物线部分是否存在这样的点
上方的抛物线部分是否存在这样的点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形和
为顶点的三角形和![]() 相似?若存在,求出此时
相似?若存在,求出此时![]() 的值,并直接判断
的值,并直接判断![]() 的形状;若不存在,请说明理由。
的形状;若不存在,请说明理由。
科目:czsx 来源: 题型:
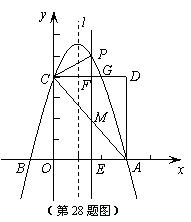
如图,抛物线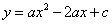 (
(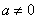 )交
)交 轴于
轴于 、
、 两点,
两点, 点坐标为(3,0),与
点坐标为(3,0),与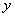 轴交于点
轴交于点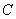 (0,4),以
(0,4),以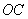 、
、 为边作矩形
为边作矩形 交抛物线于点
交抛物线于点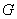 。
。
(1)求抛物线的解析式;
(2)抛物线的对称轴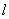 在边
在边 (不包括
(不包括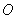 、
、 两点)上平行移动,分别交
两点)上平行移动,分别交 轴于点
轴于点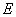 ,交
,交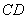 于
于 点
点 ,交
,交 于点
于点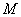 ,交抛物线于点
,交抛物线于点 ,若点
,若点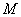 的横坐标为
的横坐标为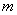 ,请用含
,请用含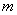 的代数式表示
的代数式表示 的长。
的长。
(3)在(2)的条件下,连结 ,则在
,则在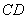 上方的抛物线部分是否存在这样的点
上方的抛物线部分是否存在这样的点 ,使得以
,使得以 、
、 、
、 为顶点的三角形和
为顶点的三角形和 相似?若存在,求出此时
相似?若存在,求出此时 的值,并直接判断
的值,并直接判断 的形状;若不存在,请说明理由
的形状;若不存在,请说明理由
科目:czsx 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:044
如图,抛物线y=ax2+bx+c的顶点为A(4,4),且抛物线经过原点,和x轴相交于另一点B,以AB为一边在直线AB的右侧画正方形ABCD.
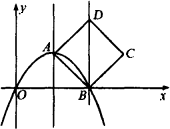
(1)求抛物线的解析式和点C、D的坐标.
(2)能否将此抛物线沿着直线x=4平移,使平移后的抛物线恰好经过正方形ABCD的另两个顶点C、D?若能,写出平移后抛物线的解析式,若不能,请说明理由.
(3)若以点A(4,4)为圆心,r为半径画圆,请你探究:
①当r=________时,⊙A上有且只有一个点到直线BD的距离等于2;
②当r=________时,⊙A上有且只有三个点到直线BD的距离等于2;
③随着的变化,⊙A上到直线BD的距离等于2的点的个数也随着变化,请根据⊙A上到直线BD的距离等于2的点的个数,讨论相应的r的值或取值范围.
科目:czsx 来源: 题型:
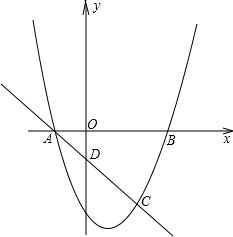 抛物线y=ax2+bx+c与x轴的交点为A(m-4,0)和B(m,0),与直线y=-x+p相交于点A和点C(2m-4,m-6).
抛物线y=ax2+bx+c与x轴的交点为A(m-4,0)和B(m,0),与直线y=-x+p相交于点A和点C(2m-4,m-6).科目:czsx 来源:四川省中考真题 题型:解答题

科目:czsx 来源: 题型:
抛物线y=ax2+bx+c与x轴的交点为A(m-4,0)和B(m,0),与直线y=-x+p相交于点A和点C(2m-4,m-6).
(1)求抛物线的解析式;
(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形ACQP面积为12,求点P,Q的坐标;
(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当⊿PQM的面积最大时,请求出⊿PQM的最大面积及点M的坐标。

科目:czsx 来源:2013年四川省广安市邻水县梁板乡中中考数学模拟试卷(一)(解析版) 题型:解答题
科目:czsx 来源:2013年四川省宜宾市中考数学模拟试卷(一)(解析版) 题型:解答题
科目:czsx 来源:2011年四川省南充市中考数学试卷(解析版) 题型:解答题
科目:czsx 来源:山东省东营市2012年中考数学试题 题型:044
已知抛物线![]() 经过A(2,0).设顶点为点P,与x轴的另一交点为点B.
经过A(2,0).设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线y=![]() x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
x上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;

(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
科目:czsx 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:填空题
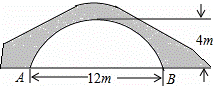
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是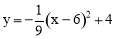 ,则选取点B为坐标原点时的抛物线解析式是 .
,则选取点B为坐标原点时的抛物线解析式是 .

科目:czsx 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:填空题
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 ..
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 ..

科目:czsx 来源: 题型:
 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=-
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=-| 1 |
| 9 |
科目:czsx 来源: 题型:
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .


科目:czsx 来源: 题型:
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .

科目:czsx 来源: 题型:
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向 为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣
为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .

科目:czsx 来源: 题型:
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .

科目:czsx 来源: 题型:
 (1)求抛物线的解析式,并求出顶点A的坐标.
(1)求抛物线的解析式,并求出顶点A的坐标.
(2) 连结AB,平移AB所在的直线,使其经过原点O,得到直线![]() .点
.点![]() 是
是![]() 上一动点,当△
上一动点,当△![]() 的周长最小时,求点P的坐标.
的周长最小时,求点P的坐标.
(3)当△![]() 的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)
的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)
科目:czsx 来源:2014-2015学年山东省滕州市九年级学业水平质量检测二数学试卷(解析版) 题型:解答题
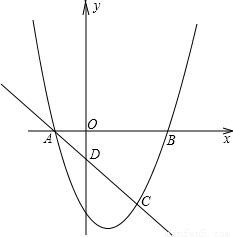
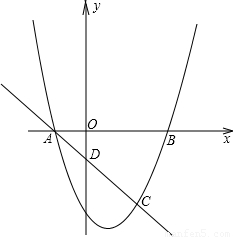
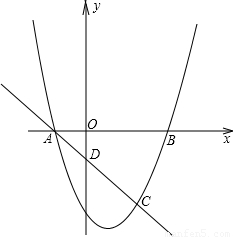
(13分)抛物线y=ax2+bx+c与x轴的交点为A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和点C(2m﹣4,m﹣6).
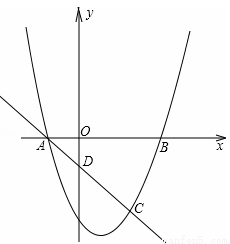
(1)求抛物线的解析式;
(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形面积为12,求点P,Q的坐标;
(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当△PQM的面积最大时,请求出△PQM的最大面积及点M的坐标.
科目:czsx 来源: 题型: