如图.已知rt△abc≌rt△ade.∠abc=∠ade=90°答案解析
科目:czsx
来源:
题型:
已知Rt△ABC,∠BAC=90°,∠C=30°,BC=8cm,将Rt△ABC绕点A顺时针旋转90°.后得到Rt△ADE(如图1).
(Ⅰ)将Rt△ABC绕点A顺时针旋转得到Rt△AB
1C
1.AC
1交DE于点F,当△AEF为等腰三角形时,旋转角的度数为
;
(Ⅱ)将Rt△DAE沿AB方向平移,得到Rt△D
2A
2E
2(如图3),E
2D
2交AC于点P.A
2D
2交BC于点N,当NP∥AB时,平移距离为
cm.

查看答案和解析>>
科目:czsx
来源:
题型:
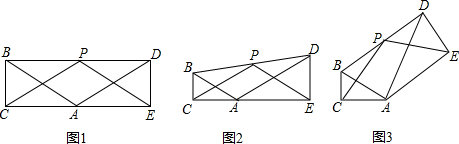
已知Rt△ABC和Rt△ADE,∠ACB=∠AED=90°,∠BAC=∠DAE=30°,P为线段BD的中点,连接PC,PE.
(1)如图1,若AC=AE,C、A、E依次在同一条直线上,则∠CPE=
;PC与PE存在的等量关系是
;
(2)如图2,若AC≠AE,C、A、E依次在同一条直线上,猜想∠CPE的度数及PC与PE存在的等量关系,并写出你的结论;(不需要证明)
;
(3)如图3,在图2的基础上,若将Rt△ADE绕点A逆时针任意旋转一个角度,使C、A、E不在一条直线上,试探究∠CPE的度数及PC与PE存在的等量关系,写出你的结论并说明理由.
查看答案和解析>>
科目:czsx
来源:2016届河南中考数学押题试卷数学试卷(解析版)
题型:解答题
已知Rt△ABC,AB=AC,∠BAC=90°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作Rt△ADE,AD=AE,连接CE.
(1)发现问题
如图①,当点D在边BC上时,
①请写出BD和CE之间的数量关系为________,位置关系为________;
②线段CE+CD=________AC;
(2)尝试探究
如图②,当点D在边BC的延长线上且其他条件不变时,(1)中AC、CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;
(3)拓展延伸
如图③,当点D在边CB的延长线上且其他条件不变时,若BC=4,CE=2,求线段CD的长.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
1.

如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.
(1)求证:DE是⊙O的切线;
(2)已知AC=6,tan∠ABC=$\frac{3}{4}$,则△ADE的周长是$\frac{48}{5}$,其面积是$\frac{54}{5}$.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
14.已知Rt△ABC,AB=AC,∠BAC=90°,点D为直线BC上的一动点(点D不与点B、C重合),以AD为边作Rt△ADE,AD=AE,连接CE.

(1)发现问题
如图①,当点D在边BC上时,
①请写出BD和CE之间的数量关系为相等,位置关系为垂直;
②线段CE+CD=$\sqrt{2}$AC;
(2)尝试探究
如图②,当点D在边BC的延长线上且其他条件不变时,(1)中AC、CE、CD之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;
(3)拓展延伸
如图③,当点D在边CB的延长线上且其他条件不变时,若BC=4,CE=2,求线段CD的长.
查看答案和解析>>
科目:czsx
来源:
题型:
如图(1),在Rt△ABC中,∠B=90°,AE平分∠BAC,将AB沿AE折叠,使点B落在AC上一点D处,已知AB=6,BC=8,可用下面的方法求线段BE的长:
由折叠可知:AD=AB=6,BE=DE,∠ADE=∠ABE=90°
在Rt△ABC中,∠B=90°,∴AC
2=AB
2+BC
2=6
2+8
2=100
∴AC=10,CD=AC-AD=4,设BE=DE=x,则CE=8-x
在Rt△CED中,∠EDC=90°,∴EC
2=ED
2+CD
2,即(8-x)
2=x
2+4
2,整理得:64-16x=16
解得:x=3
仿上面的解答法解答下题:
如图(2),在矩形ABCD中,AB=5cm,AD=13cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,求DE的长度.

查看答案和解析>>
科目:czsx
来源:
题型:
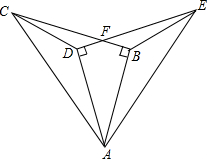
如图,已知在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,AC=AE,AD=AB,BC与DE相交于点F,连接CD,EB.
(1)图中有几对全等三角形,请你一一列举(不要说理).
(2)求证:CF=EF.
查看答案和解析>>
科目:czsx
来源:
题型:
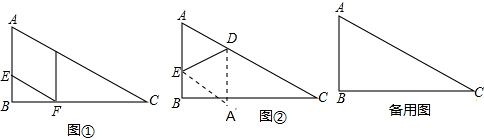
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
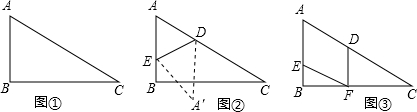
(1)试用含t的式子表示AE、AD的长;
(2)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)连接DE,当t为何值时,△DEF为直角三角形?
(4)如图②,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形 AEA′D为菱形?并判断此时点A是否在BC上?请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:在Rt△ABC中,AB=BC.在Rt△ADE中,AD=DE;连接EC,取EC中点M,连接DM和BM.
(1)若点D在边AC上,点E在边AB上且与点B不重合,如图(1),猜想BM与DM的关系;
(2)如果将图(1)中的Rt△ADE绕点A逆时针旋转90°的角,如图(2),那么(1)中的结论是否仍然成立?如果不成立,请举出反例;如果成立,请给予证明.
(3)如果将图(1)中的Rt△ADE绕点A逆时针旋转大于90°且小于135°的角,如图(3),那么(1)中的结论是否仍然成立?如果不成立,请举出反例;如果成立,请给予证明.
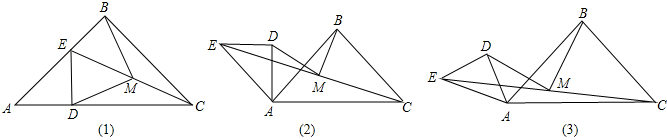
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(2)连接DE,当t为何值时,△DEF为直角三角形?
(3)如图②,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形 AEA′D为菱形?
查看答案和解析>>
科目:czsx
来源:
题型:
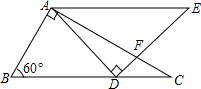
已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°,∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
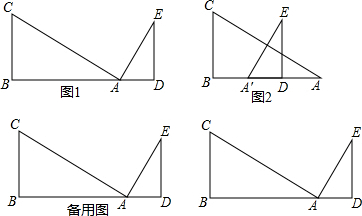
已知,Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,∠CAB=30°,∠DAE=60°,AD=3,AB=
6,且AB,AD在同一直线上,把图1中的△ADE沿射线AB平移,记平移中的△ADE为△A′DE(如图2),且当点D与点B重合时停止运动,设平移的距离为x.
(1)当顶点E恰好移动到边AC上时,求此时对应的x值;
(2)在平移过程中,设△A′DE与Rt△ABC重叠部分的面积为S,请直接写出S与x之间的函数关系式以及相应的自变量x的取值范围;
(3)过点C作CF∥AE交AB的延长线于点F,点M为直线BC上一动点,连接FM,得到△MCF,将△MCF绕点C逆时针旋转60°,得到△M′CF′(M的对应点为M′,F的对应点为F′),问△FMM′的面积能否等于
?若能,请求AM′的长度,若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:2010年广西南宁市中等学校招生考试数学试题
题型:044
如图,已知Rt△ABC≌△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连接CD,EB.
(1)图中还有几对全等三角形,请你一一列举.
(2)求证:CF=EF.

查看答案和解析>>
科目:czsx
来源:
题型:
已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°, ∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.

(此题4分)
查看答案和解析>>
科目:czsx
来源:
题型:
已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°, ∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.

(此题4分)
查看答案和解析>>
科目:czsx
来源:2014届江苏省海门市八年级下学期期末考试数学试卷(解析版)
题型:解答题
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.

(1)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(2)连接DE,当t为何值时,△DEF为直角三角形?
(3)如图②,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形 AEA′D为菱形?
查看答案和解析>>
科目:czsx
来源:2014届江苏江阴青阳中学七年级下学期期中数学试卷(解析版)
题型:解答题
已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°, ∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.

(此题4分)
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)如图②,连接DE,当t为何值时,△DEF为直角三角形?
(4)如图③,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?
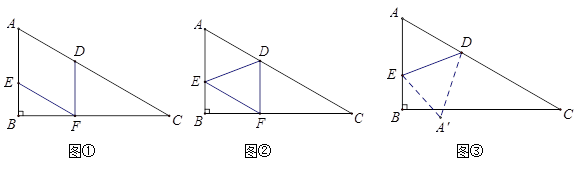
查看答案和解析>>
科目:czsx
来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版)
题型:解答题
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)如图②,连接DE,当t为何值时,△DEF为直角三角形?
(4)如图③,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?

查看答案和解析>>
科目:czsx
来源:
题型:解答题
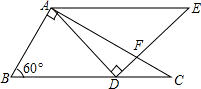 已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°,∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.
已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°,∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.
查看答案和解析>>




 如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.

 如图,已知在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,AC=AE,AD=AB,BC与DE相交于点F,连接CD,EB.
如图,已知在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,AC=AE,AD=AB,BC与DE相交于点F,连接CD,EB.


 已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°,∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.
已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°,∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.







 已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°,∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.
已知如图,Rt△ABC和Rt△DAE中,∠BAC=90°,∠ADE=90°,∠B=60°,∠E=45°,且AE∥BC,边AC与边DE交于点F,求∠AFD的度数.