练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知|x+2|+(y+5)2=0

    已知|x+2|+(y+5)2=0答案解析

    科目：gzsx 来源： 题型：

    已知|x|≤
    π
    2
    ，|y|≤
    π
    2
    ，其中满足：“x≥0，y≥0，且y≤cosx”的概率为
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知x，y满足0≤x≤
    		4-y2
    ，则
    y-2
    x-3
    的取值范围是
    [0，
    12
    5
    ]
    [0，
    12
    5
    ]
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知
    x≥1
    2x-y-2≤0
    x-y+1≥0
    ，则2x+y的最小值是（　　）

    查看答案和解析>>

    科目：gzsx 来源：2015届广东省高一暑假作业（四）必修2数学试卷（解析版） 题型：选择题

    已知M (-2,0), N (2,0), 则以MN为斜边的直角三角形直角顶点P的轨迹方程是(   )

    A．

    B．

    C．

    D．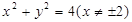

     

    查看答案和解析>>

    科目：gzsx 来源：2011-2012年吉林省松原市高二上学期12月考试理数 题型：选择题

    已知M(-2,0),N(2,0)，|PM|-|PN|=4，则动点P的轨迹是

    A.双曲线          B.双曲线左支        C.双曲线右支        D.一条射线

     

    查看答案和解析>>

    科目：gzsx 来源：2013届山东省高二12月份月考理科数学试卷 题型：选择题

    已知M(-2,0),N(2,0)，|PM|-|PN|=4，则动点P的轨迹是（    ）

    A.双曲线            B.双曲线左支        C.双曲线右支        D.一条射线

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：单选题

    已知M (-2,0), N (2,0), 则以MN为斜边的直角三角形直角顶点P的轨迹方程是(   )

    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：gzsx 来源：2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷（解析版） 题型：选择题

    已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为(　　)

    (A)x2+y2=2 (B)x2+y2=4

    (C)x2+y2=2(x≠±2) (D)x2+y2=4(x≠±2)

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知F1(-2,0),F2(2,0)，点P满足|PF1|-|PF2|=2λ(λ为常数且0＜λ≠2).

    (1)求P点的轨迹曲线E的方程；

    (2)当0＜λ＜2时，过点M(-λ，0)作两直线l1、l2与曲线E相交于A、B两点，若MA·MB=0且AB恒过点F2(2，0)时，求λ的值.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知F1(-2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为E.

    (1)求轨迹E的方程;

    (2)若直线l过点F2且与轨迹E交于P、Q两点,①无论直线l绕F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.②过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,是否存在直线l,满足|PA|+|QB|=|AB|,若存在,求出l的方程;若不存在,请说明理由.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知F1(-2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为E.

    (1)求轨迹E的方程;

    (2)若直线l过点F2且与轨迹E交于P、Q两点.①无论直线l绕F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立.求实数m的值.②过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,是否存在直线l,满足|PA|+|QB|=|AB|,若存在,求出l的方程;若不存在,请说明理由.

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：单选题

    已知M (-2,0), N (2,0), 则以MN为斜边的直角三角形直角顶点P的轨迹方程是(   )
    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知M (-2,0), N (2,0), 则以MN为斜边的直角三角形直角顶点P的轨迹方程是(   )

    A.                 B.     

    C.                  D.  

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知M (-2,0), N (2,0), 则以MN为斜边的直角三角形直角顶点P的轨迹方程是(   )

    (A)                 (B)

    (C)         (D)

    查看答案和解析>>

    科目：gzsx 来源： 题型：单选题

    已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为(　　)

    A．x2+y2=2 B．x2+y2=4
    C．x2+y2=2(x≠±2) D．x2+y2=4(x≠±2)

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知x，y满足
    0≤x≤3
    0≤y≤4
    x-y≤0
    ，则
    		(x-2)2+(y+1)2
    的最小值为（　　）
    A、
    		5
    B、
    3
    		2
    2
    C、
    		3
    6
    D、
    		17

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （已知(
    		x
    +
    2
    3a2
    )n(0＜a＜1)    的展开式中第五项与第三项的二项式系数之比为15：2，求：（1）T4；（2）满足T4＜1760xlogax的x的取值范围．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    （已知(
    		x
    +
    2
    3a2
    )n(0＜a＜1)    的展开式中第五项与第三项的二项式系数之比为15：2，求：（1）T4；（2）满足T4＜1760xlogax的x的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    (理)已知F1(-2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为E.

    (1)求轨迹E的方程;

    (2)若直线l过点F2且与轨迹E交于P、Q两点.

    ①无论直线l绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.

    ②过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=,求λ的取值范围.

    (文)已知等差数列{an}中,a1=-2,a2=1.

    (1)求{an}的通项公式;

    (2)调整数列{an}的前三项a1、a2、a3的顺序,使它成为等比数列{bn}的前三项,求{bn}的前n项和.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （08年赤峰二中模拟理） 已知F1(- 2, 0), F2 (2, 0), 点P满足| PF1| - | PF2| = 2, 记点P的轨迹为E.

    (Ⅰ) 求轨迹E的方程；

    (Ⅱ) 若直线l过点F2且与轨迹E交于P、Q两点,

    ①无论直线l绕点F2怎样转动, 在x轴上总存在定点M(m, 0), 使MP ^ MQ恒成立, 求实数m的值;

    ②过P、Q作直线x =的垂线PA、QB, 垂足分别为A、B, 记l =, 求l的取值范围.

    查看答案和解析>>