
科目:gzsx 来源: 题型:解答题
 如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD.
如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD.科目:gzsx 来源:2012年普通高等学校招生全国统一考试山东卷数学文科 题型:044
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.

(Ⅰ)求证:BE=DE;
(Ⅱ)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
科目:gzsx 来源: 题型:
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.

科目:gzsx 来源: 题型:
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.

(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
科目:gzsx 来源: 题型:
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1) 求证:BE=DE;
(2) 若∠BCD=120°,M为线段AE的中点,
求证:DM∥平面BEC.
 |
科目:gzsx 来源:山东省高考真题 题型:证明题

科目:gzsx 来源:2012-2013学年山东省淄博市桓台二中高二(下)期初数学试卷(解析版) 题型:解答题

科目:gzsx 来源:2012-2013学年吉林省白山市长白山一高高一(上)综合检测数学试卷(解析版) 题型:解答题

科目:gzsx 来源:2012-2013学年山东省济宁市泗水一中高二(下)期中数学试卷(理科)(解析版) 题型:解答题

科目:gzsx 来源:2012-2013学年陕西省咸阳市武功县高三(上)摸底数学试卷(文科)(解析版) 题型:解答题

科目:gzsx 来源:2012-2013学年山东省济宁市兖州市高三(上)入学检测数学试卷(文科)(解析版) 题型:解答题

科目:gzsx 来源:2012-2013学年甘肃省白银市平川中恒学校高三(上)第一次月考数学试卷(解析版) 题型:解答题

科目:gzsx 来源:2012年山东省高考数学试卷(文科)(解析版) 题型:解答题

科目:gzsx 来源: 题型:解答题
 如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.科目:gzsx 来源: 题型:
[2012·山东卷] 如图1-6,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
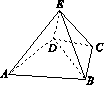
图1-6
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
科目:gzsx 来源: 题型:
[2012·山东卷] 如图1-6,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.

图1-6
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
科目:gzsx 来源: 题型:
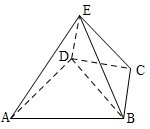 (2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.