精英家教网 >
试题搜索列表 >已知矩形abcd.ab=8.bc=6,e为ad边上一点.过a.b.e三点作⊙o
已知矩形abcd.ab=8.bc=6,e为ad边上一点.过a.b.e三点作⊙o答案解析
科目:czsx
来源:2016届浙江省九年级下学期学科素养测试数学试卷(解析版)
题型:解答题
已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE、CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于H.

(Ⅰ)当直线FH与⊙O相切时,求AE的长;
(Ⅱ)若直线FH交⊙O于点G,
(ⅰ)当FH∥BE时,求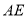 的长;
的长;
(ⅱ)在点E运动过程中,△OFG能否成为等腰直角三角形?如果能,求出此时AE的长;如果不能,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
10.如图1所示,已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE、CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于点H,直线FH交⊙O于点G.

(1)如图2所示,当点E为AD的中点时,求证:FH为⊙O的切线;
(2)当FH∥BE,求FG的长;
(3)在点E的运动过程中,当AE≤$\frac{1}{2}$AD时,△OFG能否成为等腰直角三角形?如果能,求出此时AE的长;如果不能,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP,
(1)求证:BE是⊙O的直径且OP⊥AB;
(2)若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;
(3)如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.
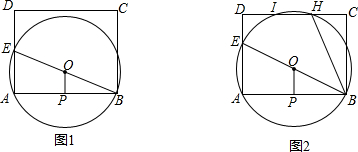
查看答案和解析>>
科目:czsx
来源:
题型:解答题
18.

如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.
查看答案和解析>>
科目:czsx
来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版)
题型:解答题
(本题满分12分)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;(提示:直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角为300)
(3)如图2,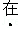


 ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:czsx
来源:
题型:

已知在矩形ABCD中,P是边AD上的一动点,联结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y;
(1)求y关于x的函数解析式,并写出它的定义域;
(2)当AP=4时,求∠EBP的正切值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长.
查看答案和解析>>
科目:czsx
来源:
题型:
已知在矩形ABCD中,P是边AD上的一动点,联结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y;
(1)求y关于x的函数解析式,并写出 它的定义域;
它的定义域;
(2)当AP=4时,求∠EBP的正切值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长.

查看答案和解析>>
科目:czsx
来源:
题型:
已知,矩形纸片ABCD中,AB=10cm,AD=8cm,按下列步骤进行操作:

如图1,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);
如图2,沿三角形EBC的中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;
如图3,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180°,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等的四边形纸片.(注:裁剪和拼图过程均无缝且不重叠)
发现:(1)通过操作,最后拼成的四边形形状为
;
探究:(2)由于题中点E、M、N的位置不确定,因而所得四边形的周长会发生变化,探究下列问题:
①拼成的四边形的周长取决于线段
的长;
②通过操作发现,四边形的周长存在最大值和最小值,请在图4和图5中分别画出相应的剪拼图并直接写出该四边形的周长最值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
5.

已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
(1)求y关于x的函数解析式;
(2)当AP=4时,求∠EBP的正切值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
6.已知,矩形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行操作:
如图1在线段AD上任意取一点E,沿EB、EC剪下一个三角形纸片EBC(余下部分不再使用);如图2,沿三角形EBC的中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;如图3,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180°,使线段HC与HE重合,拼成一个与三角形纸片EBC面积相等的四边形纸片.(注:裁剪和拼图过程均无缝且不重叠)
(1)通过操作,最后拼成的四边形为平行四边形.
(2)拼成的这个四边形的周长的最小值为20cm,最大值为12+$4\sqrt{13}$cm.

查看答案和解析>>
科目:czsx
来源:
题型:
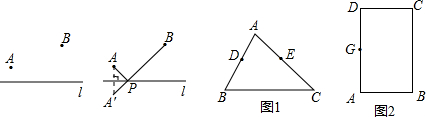
(2012•通州区一模)小明在学习轴对称的时候,老师留了这样一道思考题:如图,已知在直线l的同侧有A、B两点,请你在直线l上确定一点P,使得PA+PB的值最小.小明通过独立思考,很快得出了解决这个问题的正确方法,他的作法是这样的:
①作点A关于直线l的对称点A′.
②连接A′B,交直线l于点P.则点P为所求.请你参考小明的作法解决下列问题:
(1)如图1,在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使得△PDE的周长最小.
①在图1中作出点P.(三角板、刻度尺作图,保留作图痕迹,不写作法)
②请直接写出△PDE周长的最小值
8
8
.
(2)如图2在矩形ABCD中,AB=4,BC=6,G为边AD的中点,若E、F为边AB上的两个动点,点E在点F左侧,且EF=1,当四边形CGEF的周长最小时,请你在图2中确定点E、F的位置.(三角板、刻度尺作图,保留作图痕迹,不写作法),并直接写出四边形CGEF周长的最小值
.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
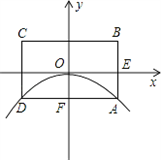
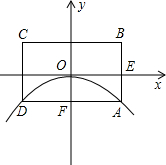 如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(1)求此抛物线的解析式.
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状.
查看答案和解析>>
科目:czsx
来源:湖南省中考真题
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状。
查看答案和解析>>
科目:czsx
来源:2012年初中毕业升学考试(湖南衡阳卷)数学(带解析)
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
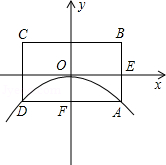
(1)求此抛物线的解析式.
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状.
查看答案和解析>>
科目:czsx
来源:2013届山东省济南市长清区九年级学业水平模拟考试数学试卷(带解析)
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A、D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O).
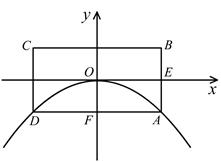
(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R;
①求证:PF=PR
②是否存在点P,使得△PFR为等边三角形;若存在,求出点P的坐标,若不存在,请说明理由.
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为点S,试判断△RSF的形状.
查看答案和解析>>
科目:czsx
来源:2013年山东省济南市长清区中考数学二模试卷(解析版)
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(1)求此抛物线的解析式.
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状.
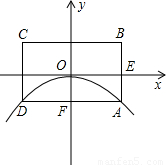
查看答案和解析>>
科目:czsx
来源:2013年江西省宜春市樟树市中考数学模拟试卷(二)(解析版)
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(1)求此抛物线的解析式.
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状.
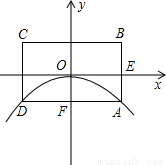
查看答案和解析>>
科目:czsx
来源:2012年湖南省衡阳市中考数学试卷(解析版)
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(1)求此抛物线的解析式.
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状.

查看答案和解析>>
科目:czsx
来源:2012-2013学年山东省济南市长清区九年级学业水平模拟考试数学试卷(解析版)
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A、D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O).

(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R;
①求证:PF=PR
②是否存在点P,使得△PFR为等边三角形;若存在,求出点P的坐标,若不存在,请说明理由.
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为点S,试判断△RSF的形状.
查看答案和解析>>
科目:czsx
来源:2012年初中毕业升学考试(湖南衡阳卷)数学(解析版)
题型:解答题
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)

(1)求此抛物线的解析式.
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状.
查看答案和解析>>


 的长;
的长;
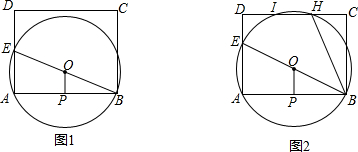
 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
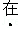

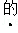

 ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度. 已知在矩形ABCD中,P是边AD上的一动点,联结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y;
已知在矩形ABCD中,P是边AD上的一动点,联结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y; 它的定义域;
它的定义域;

 已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y

 如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)