科目：czsx 来源： 题型：解答题
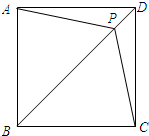如图，点P是正方形ABCD的对角线BD上一点，连接PA、PC．科目：czsx 来源：2010年黑龙江省大庆市中考数学试卷（解析版） 题型：解答题
科目：gzsx 来源： 题型：
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC;
(3)求二面角A-EC-P的大小.
科目：czsx 来源： 题型：
24、如图，点P是正方形ABCD的对角线BD上一点，连接PA、PC．科目：gzsx 来源： 题型：
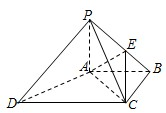如图，四棱锥P-ABCD中，PA⊥底面ABCD，PC⊥AD．底面ABCD为梯形，AB∥DC，AB⊥BC．PA=AB=BC，点E在棱PB上，且PE=2EB．科目：gzsx 来源： 题型：
如图，四棱锥P-ABCD中，PA⊥底面ABCD，PC⊥AD．底面ABCD为梯形，AB∥DC，AB⊥BC，PA=AB=BC，点E在棱PB上，且PE=2EB．科目：gzsx 来源： 题型：解答题
如图，四棱锥P-ABCD中，PA⊥底面ABCD，PC⊥AD．底面ABCD为梯形，AB∥DC，AB⊥BC，PA=AB=BC，点E在棱PB上，且PE=2EB．科目：gzsx 来源：2012-2013学年江苏省苏州市张家港市梁丰高级中学高三（上）期末数学模拟试卷（一）（解析版） 题型：解答题
科目：gzsx 来源：2010-2011学年山东省济南市高三（上）12月质量调研数学试卷A（理科）（解析版） 题型：解答题
科目：gzsx 来源：2013年高考数学复习卷C（三）（解析版） 题型：解答题
科目：gzsx 来源：2012年江苏省南通市海安县曲塘中学高考数学考前最后一卷（解析版） 题型：解答题
科目：gzsx 来源：2011年四川省眉山市高考数学一模试卷（理数）（解析版） 题型：解答题
科目：gzsx 来源：2011年四川省眉山市高考数学一模试卷（文科）（解析版） 题型：解答题
科目：gzsx 来源：2008年北京市海淀区高考数学一模试卷（理科）（解析版） 题型：解答题
科目：gzsx 来源： 题型：解答题
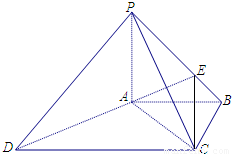
如图，在四棱锥PABCD中，PA⊥底面ABCD，PC⊥AD，底面ABCD为梯形，AB∥DC，AB⊥BC，PA＝AB＝BC，点E在棱PB上，且PE＝2EB.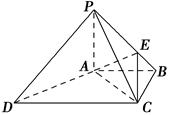
(1)求证：平面PAB⊥平面PCB；
(2)求证：PD∥平面EAC.
科目：gzsx 来源：不详 题型：解答题
科目：gzsx 来源：2013-2014学年高考数学（文）三轮专题体系通关训练解答题押题练B组练习卷（解析版） 题型：解答题
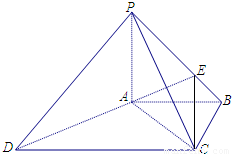
如图，在四棱锥P ABCD中，PA⊥底面ABCD，PC⊥AD，底面ABCD为梯形，AB∥DC，AB⊥BC，PA＝AB＝BC，点E在棱PB上，且PE＝2EB.
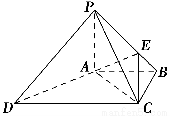
(1)求证：平面PAB⊥平面PCB；
(2)求证：PD∥平面EAC.
科目：gzsx 来源： 题型：
如图，在四棱锥P ABCD中，PA⊥底面ABCD，PC⊥AD，底面ABCD为梯形，AB∥DC，AB⊥BC，PA＝AB＝BC，点E在棱PB上，且PE＝2EB.
(1)求证：平面PAB⊥平面PCB；
(2)求证：PD∥平面EAC.
科目：czsx 来源： 题型：
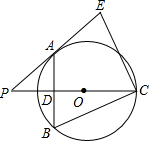如图，PC经过圆心O，弦AB⊥PC于点D．连接BC和PA，且∠PAB=2∠PCB．| 1 |
| 3 |
科目：czsx 来源： 题型：
如图，P是边长为1的正方形ABCD对角线BD上一动点（P与B、D不重合），∠APE=90°，且点E在BC边上，AE交BD于点F．| AP |
| AE |