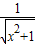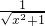精英家教网 >
试题搜索列表 >定义在R上的函数f(x)满足f(1)=1,且对任意x∈R,都有f′(x)< 1 2 ,则不等式f(x2)> x2+1 2 的解集
定义在R上的函数f(x)满足f(1)=1,且对任意x∈R,都有f′(x)< 1 2 ,则不等式f(x2)> x2+1 2 的解集答案解析
科目:gzsx
来源:
题型:
已知函数
g(x)=(x≠0,x≠±1,x∈R)的值域为A,定义在A上的函数f(x)=x
-2-x
2(x∈A).
(1)判断函数f(x)的奇偶性;
(2)判断函数f(x)的单调性并用定义证明;
(3)解不等式f(3x+1)>f(5x+1).
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在D上的函数f(x),如果满足:对∀x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数.则下列定义在R上的函数中,不是有界函数的是( )
| |
| |
查看答案和解析>>
科目:gzsx
来源:
题型:
已知集合A={x|2≤x≤π,x∈R},定义在A上的函数f(x)=log
ax(a>0,且a≠1)的最大值比最小值大1,则底数a的值是( )
A. B.
B.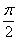 C.
C. 或
或 D.2π
D.2π
查看答案和解析>>
科目:gzsx
来源:不详
题型:单选题
定义在D上的函数f(x),如果满足:对∀x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数.则下列定义在R上的函数中,不是有界函数的是( )
| A.f(x)=sinx2 | B.f(x)= |
| C.f(x)=-21-|x| | D.f(x)=-log2(|x|+1) |
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知函数
g(x)=(x≠0,x≠±1,x∈R)的值域为A,定义在A上的函数f(x)=x
-2-x
2(x∈A).
(1)判断函数f(x)的奇偶性;
(2)判断函数f(x)的单调性并用定义证明;
(3)解不等式f(3x+1)>f(5x+1).
查看答案和解析>>
科目:gzsx
来源:2012-2013学年湖北省黄冈中学、孝感高中高三(上)期末数学试卷(文科)(解析版)
题型:选择题
定义在D上的函数f(x),如果满足:对∀x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数.则下列定义在R上的函数中,不是有界函数的是( )
A.f(x)=sinx
2B.f(x)=
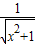
C.f(x)=-2
1-|x|D.f(x)=-log
2(|x|+1)
查看答案和解析>>
科目:gzsx
来源:
题型:单选题
定义在D上的函数f(x),如果满足:对∀x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数.则下列定义在R上的函数中,不是有界函数的是
- A.
f(x)=sinx2
- B.
f(x)=
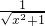
- C.
f(x)=-21-|x|
- D.
f(x)=-log2(|x|+1)
查看答案和解析>>
科目:gzsx
来源:
题型:
设定义在N上的函数f(n)满足f(n)=
| | n+13 ,n≤2000 | | f[f(n-18)] ,n>2000 |
| |
则f(2003)=
2011
2011
.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.
举例:f(x)=x,D=[-3,2],则对任意x∈D,|f(x)|≤3,根据上述定义,f(x)=x在[-3,2]上为有界函数,上界可取3,5等等.
已知函数f(x)=1+a•2
x+4
x,g(x)=
.
(1)当a=1时,求函数f(x)在(0,+∞)上的值域,并判断函数f(x)在(0,+∞)上是否为有界函数,请说明理由;
(2)求函数g(x)在[0,1]上的上界T的取值范围;
(3)若函数f(x)在(-∞,0]上是以3为上界的函数,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
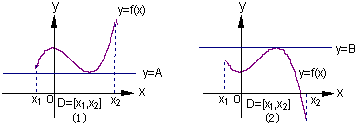
(2007•揭阳二模)如图(1)示,定义在D上的函数f(x),如果满足:对∀x∈D,∃常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图(1)、(2)中的常数A、B可以是正数,也可以是负数或零)
(Ⅰ)试判断函数f(x)=x
3+
在(0,+∞)上是否有下界?并说明理由;
(Ⅱ)又如具有如图(2)特征的函数称为在D上有上界.请你类比函数有下界的定义,给出函数f(x)在D上有上界的定义,并判断(Ⅰ)中的函数在(-∞,0)上是否有上界?并说明理由;
(Ⅲ)若函数f(x)在D上既有上界又有下界,则称函数f(x)在D上有界,函数f(x)叫做有界函数.试探究函数f(x)=ax
3+
(a>0,b>0a,b是常数)是否是[m,n](m>0,n>0,m、n是常数)上的有界函数?
查看答案和解析>>
科目:gzsx
来源:
题型:
(2007•揭阳二模)如图(1)示,定义在D上的函数f(x),如果满足:对∀x∈D,∃常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图(1)、(2)中的常数A、B可以是正数,也可以是负数或零)

(Ⅰ)试判断函数f(x)=x
3+
在(0,+∞)上是否有下界?并说明理由;
(Ⅱ)又如具有如图(2)特征的函数称为在D上有上界.请你类比函数有下界的定义,给出函数f(x)在D上有上界的定义,并判断(Ⅰ)中的函数在(-∞,0)上是否有上界?并说明理由;
(Ⅲ)已知某质点的运动方程为S(t)=at-2
,要使在t∈[0,+∞)上的每一时刻该质点的瞬时速度是以A=
为下界的函数,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界、若函数f(x)=1+a•
()x+
()x在[0,+∞)上是以3为上界的有界函数,则实数a的取值范围是( )
| A、[-5,0] |
| B、[-4,1] |
| C、[-4,0] |
| D、[-5,1] |
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M 成立,则称f(x)是D上的有界函数,其中M称为函f(x)的一个上界.
已知函数f(x)=1+a
()x+
()x,g(x)=
log.
(1)若函数g(x)为奇函数,求实数a的值;
(2)在(1)的条件下,求函数g(x),在区间[
,3]上的所有上界构成的集合;
(3)若函数g(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在D上的函数f(x),如果满足;对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数f(x)=1+a•2
x+4
x,g(x)=
.
(1)当a=1时,求函数f(x)在(0,+∞)上的值域,并判断函数f(x)在(0,+∞)上是否为有界函数,请说明理由;
(2)求函数g(x)在[0,1]上的上界T的取值范围;
(3)若函数f(x)在(-∞,0]上是以3为上界的函数,求实数a的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
(文)已知
A={x|≤x≤2},f(x)=x
2+px+q和
g(x)=x++1是定义在A上的函数,当x、x
0∈A时,有f(x)≥f(x
0),g(x)≥g(x
0),且f(x
0)=g(x
0),则f(x)在A上的最大值是
4
4
.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数
f(x)=1+a•()x+()x;
g(x)=(1)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围;
(2)已知m>-1,函数g(x)在[0,1]上的上界是T(m),求T(m)的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在D上的函数f(x)如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数
f(x)=.
(1)m=1时,求函数f(x)在(-∞,0)上的值域,并判断f(x)在(-∞,0)上是否为有界函数,请说明理由;
(2)若函数f(x)在[0,1]上是以3为上界的有界函数,求m的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
定义在N
+上的函数f(x),满足f(n+1)=
,
(1)若f(11)=
,则f(1)
.
(2)若f(1)=1,则f(2
n)=
(用含n的式子表示).
查看答案和解析>>
科目:gzsx
来源:
题型:
已知a>0,定义在D上的函数f(x)和g(x)的值域依次是[-(2a+3)π
3,a+6]和
[a2+,(a2+)π4],若存在
x1,x2∈D,使得|f(x1)-g(x2)|<成立,则a的取值范围为
(0,1)
(0,1)
.
查看答案和解析>>
科目:gzsx
来源:
题型:
对于定义在D上的函数f(x),如果存在常数M和N,使得对于任意x∈D,都有M≤f(x)≤N成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的一个下界,N称为函数f(x)的一个上界.
(1)判断函数f(x)=log
2x-x
2在(0,+∞)上是否为有界函数,不必说明理由;
(2)判断函数f(x)=1+(
)
x+(
)
x在[0,+∞)上是否为有界函数,请说明理由
(3)若函数f(x)=1+a(
)
x+(
)
x在[0,+∞)上是有界函数,且3是f(x)的一个上界,-3是f(x)的一个下界,求实数a的取值范围.
查看答案和解析>>

![]() B.
B.![]() C.
C.![]() 或
或![]() D.2π
D.2π