
7.已知函数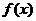 是定义在R上的奇函数,其最小正周期为3,
且
是定义在R上的奇函数,其最小正周期为3,
且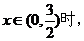


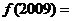
A.4
B.2
C. -2
D.
6.平面 与平面
与平面 外有一条直线
外有一条直线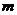 ,如果
,如果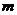 在
在 与
与 内的射影分别是直线
内的射影分别是直线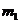 和直线
和直线
 ,给出下列四个命题:
,给出下列四个命题:
①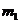 ∥
∥

 ∥
∥ ; ②
; ② ∥
∥

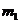 ∥
∥ ;
;
③ ⊥
⊥

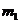 ⊥
⊥ ; ④
; ④ 与
与 相交
相交
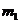 与
与 相交;
相交;
其中正确的命题个数是
A.1 B.2 C.3 D.4
5.设变量 满足约束条件
满足约束条件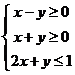 ,则
,则 的最大值为
的最大值为
A. 2 B. 4 C. 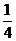 D.
D. 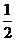
4.记等差数列 的前
的前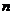 项和为
项和为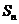 ,若
,若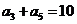 ,
, ,则直线
,则直线
的斜率为
A.-2 B. C.-
C.- D.
D.
3.已知 ,则
,则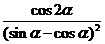 =
=
A. B.
B. C.
C. D.
D.
2.设集合 ,B=
,B=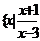 ≤0
≤0 ,那么“
,那么“ ”是“
”是“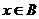 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件
1.复数 的虚部为
的虚部为
A.1 B.4 C.-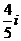 D.-
D.-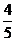
16(本题满分12分).
在锐角△ 中,内角A、B、C的对边分别为
中,内角A、B、C的对边分别为 、
、 、
、 ,且
,且
(Ⅰ)求A的值;
(Ⅱ)求 的取值范围。
的取值范围。
17(本题满分12分).设进入健身中心的每一位健身者选择甲种健身项目的概率是 ,选择乙种健身项目的概率是
,选择乙种健身项目的概率是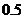 ,且选择甲种与选择乙种健身项目相互独立,各位健身者之间选择健身项目是相互独立的。
,且选择甲种与选择乙种健身项目相互独立,各位健身者之间选择健身项目是相互独立的。
(Ⅰ)求进入该健身中心的1位健身者选择甲、乙两种项目中的一项的概率;
(Ⅱ)求进入该健身中心的4位健身者中,至少有2位既未选择甲种又未选择乙种健身项目的概率。
 18(本题满分12分).
四棱锥
18(本题满分12分).
四棱锥 中,
中,

 ,
, 平面ABCD,
平面ABCD,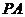 =
=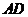 =
= =2,
=2,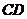 =4。
=4。
(Ⅰ)求证:平面
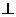 平面
平面 ;
;
(Ⅱ)求点 到平面
到平面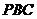 的距离;
的距离;
|
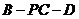 的大小。
的大小。
19(本题满分13分).
数列 的前
的前 项和为
项和为 ,点
,点 在曲线
在曲线 上。
上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列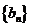 的前
的前 项和为
项和为 ,若
,若 对
对 恒成立,求最大正整数
恒成立,求最大正整数 的值。
的值。
20(本题满分13分).已知点 (4,0),直线
(4,0),直线 ,和动点
,和动点 。作
。作 ,垂足为
,垂足为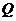 ,且向量
,且向量 ,设点
,设点 的轨迹曲线为
的轨迹曲线为 。
。
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)定义:直线被曲线所截得的线段叫做这条曲线的弦。求曲线 的以
的以 (-3,1)为中点的弦的直线方程。
(-3,1)为中点的弦的直线方程。
21(本题满分13分). 设函数 二次函数
二次函数 。
。
(Ⅰ)若 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)当函数 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最大值时,记
存在最大值时,记 的最大值为
的最大值为 ,求函数
,求函数 的解析式;
的解析式;
|
 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围。
的取值范围。
株洲市2009年高三年级教学质量统一检测(一)
15.设 分别是椭圆
分别是椭圆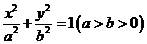 的左、右焦点,若在其左准线上存在点M,使线段MF2的中垂线过点F1,则椭圆的离心率的取值范围是_______________.
的左、右焦点,若在其左准线上存在点M,使线段MF2的中垂线过点F1,则椭圆的离心率的取值范围是_______________.
14.直线 按向量
按向量 平移后与圆
平移后与圆 相切,则实数
相切,则实数 的值为_____.
的值为_____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com