
7.(2008浙江义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
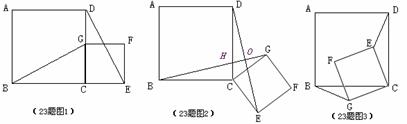
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度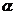 ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
 (2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka, CG=kb (a
(2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka, CG=kb (a b,k
b,k 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结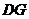 、
、 ,且a=3,b=2,k=
,且a=3,b=2,k= ,求
,求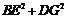 的值.
的值.
6. (2008浙江金华)如图1,在平面直角坐标系中,己知ΔAOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.(1)求直线AB的解析式;(2)当点P运动到点( ,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于
,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于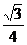 ,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

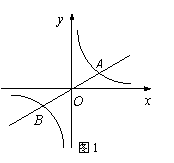
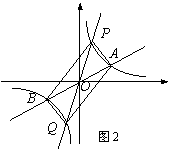
5、(2007浙江金华)如图1,已知双曲线y=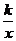 (k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;
(k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;
(2)如图2,过原点O作另一条直线l,交双曲线y=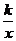 (k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行四边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出mn应满足的条件;若不可能,请说明理由.
(k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行四边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出mn应满足的条件;若不可能,请说明理由.
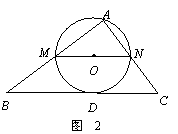
4.(08山东省日照市)在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?


3. (08浙江温州)如图,在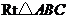 中,
中, ,
, ,
, ,
, 分别是边
分别是边 的中点,点
的中点,点 从点
从点 出发沿
出发沿 方向运动,过点
方向运动,过点 作
作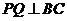 于
于 ,过点
,过点 作
作 交
交 于
于
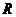 ,当点
,当点 与点
与点 重合时,点
重合时,点 停止运动.设
停止运动.设 ,
,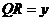 .
.
(1)求点 到
到 的距离
的距离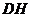 的长;
的长;
(2)求 关于
关于 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点 ,使
,使 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

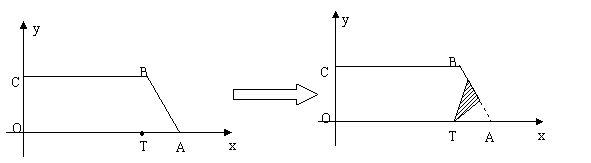
2. (08浙江衢州)已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8, ),C(0,
),C(0, ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;
(2)当纸片重叠部分的图形是四边形时,求t的取值范围;
(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由.
1.(2008年四川省宜宾市)
已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
(1) 求该抛物线的解析式;
(2) 若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;
(3) △AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为 )
)

.
23.请以《站在___________的门口》为题写一篇文章。(60分)
要求:①将题目补充完整,并写在答题卡上,然后作文。
②立意自定。
③文体不限。可以记叙经历,抒发感情,发表议论,展开想象,等等。
④不少于800字。
22.为庆祝新中国成立60周年,学样拟编辑出版诗歌征文集。现有两个备选书名《献给母亲的歌》和《山河岁月欢乐颂》,你喜欢哪一个?请写下你喜欢的书名并说明理由。(4分)
我喜欢的书名:《__________________》
理由:_____________________________________________________________________
21.下面是一段介绍王羲之书法文字,请用比较工整的语句(如排比)概括王羲之在书法史上的主要贡献。要求:①合原意。②超过30字。(4分)
在书法史上,王羲之是一位富有革新精神的大书法家。他早年从卫夫人学书,后改变初学,草书学张芝,楷书学钟繇,在书法上达到了“贵越群品,古今莫二”的高度。中晚年时,他不满当时用笔滞重、结体稚拙的局面,锐意改革,书风大变。他对楷书的结构、点画等加以变革,使楷书趋于匀称俊俏,挺拔多姿;他开创了今草,基草书用笔多变,流畅而富有韵致,比起前人有了质的飞跃;他的行书婉转灵动,俊逸妍美,从此行书取得了与篆楷草并列的地位。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com