
28. 解:(1)∵D(-8,0),∴B点的横坐标为-8,代入 中,得y=-2.
中,得y=-2.
∴B点坐标为(-8,-2).而A、B两点关于原点对称,∴A(8,2)
从而k=8×2=16
(2)∵N(0,-n),B是CD的中点,A,B,M,E四点均在双曲线上,
∴mn=k,B(-2m,- ),C(-2m,-n),E(-m,-n)
),C(-2m,-n),E(-m,-n)
 =2mn=2k,
=2mn=2k, =
= mn=
mn= k,
k, =
= mn=
mn= k.
k.
∴ =
= ―
― ―
― =k.∴k=4.
=k.∴k=4.
由直线 及双曲线
及双曲线 ,得A(4,1),B(-4,-1)
,得A(4,1),B(-4,-1)
∴C(-4,-2),M(2,2)
设直线CM的解析式是 ,由C、M两点在这条直线上,得
,由C、M两点在这条直线上,得
 ,解得a=b=
,解得a=b=
∴直线CM的解析式是y= x+
x+ .
.
(3)如图,分别作AA1⊥x轴,MM1⊥x轴,垂足分别为A1,M1
设A点的横坐标为a,则B点的横坐标为-a.于是 ,
,
同理
∴p-q= -
- =-2
=-2
27. 解:(1)由题意:BP=tcm,AQ=2tcm,则CQ=(4-2t)cm,
∵∠C=90°,AC=4cm,BC=3cm,∴AB=5cm
∴AP=(5-t)cm,
∵PQ∥BC,∴△APQ∽△ABC,
∴AP∶AB=AQ∶AC,即(5-t)∶5=2t∶4,解得:t=
∴当t为 秒时,PQ∥BC
秒时,PQ∥BC
………………2分
(2)过点Q作QD⊥AB于点D,则易证△AQD∽△ABC
∴AQ∶QD=AB∶BC
∴2t∶DQ=5∶3,∴DQ=
∴△APQ的面积: ×AP×QD=
×AP×QD= (5-t)×
(5-t)×
∴y与t之间的函数关系式为:y=
………………5分
(3)由题意:
当面积被平分时有: =
= ×
× ×3×4,解得:t=
×3×4,解得:t=
当周长被平分时:(5-t)+2t=t+(4-2t)+3,解得:t=1
∴不存在这样t的值
………………8分
(4)过点P作PE⊥BC于E
易证:△PAE∽△ABC,当PE= QC时,△PQC为等腰三角形,此时△QCP′为菱形
QC时,△PQC为等腰三角形,此时△QCP′为菱形
∵△PAE∽△ABC,∴PE∶PB=AC∶AB,∴PE∶t=4∶5,解得:PE=
∵QC=4-2t,∴2× =4-2t,解得:t=
=4-2t,解得:t=
∴当t= 时,四边形PQP′C为菱形
时,四边形PQP′C为菱形
此时,PE= ,BE=
,BE= ,∴CE=
,∴CE=
………………10分
在Rt△CPE中,根据勾股定理可知:PC= =
= =
=
∴此菱形的边长为 cm ………………12分
cm ………………12分
26. 解:方案一:由题意可得: ,
,
 点
点 到甲村的最短距离为
到甲村的最短距离为 .······································································· (1分)
.······································································· (1分)
 点
点 到乙村的最短距离为
到乙村的最短距离为 .
.
 将供水站建在点
将供水站建在点 处时,管道沿
处时,管道沿 铁路建设的长度之和最小.
铁路建设的长度之和最小.
即最小值为 .········································································ (3分)
.········································································ (3分)
方案二:如图①,作点 关于射线
关于射线 的对称点
的对称点 ,则
,则 ,连接
,连接 交
交 于点
于点 ,则
,则 .
.
 ,
, .·········································································· (4分)
.·········································································· (4分)
在 中,
中,
 ,
, ,
,
 ,
,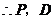 两点重合.即
两点重合.即 过
过 点.············································· (6分)
点.············································· (6分)
在线段 上任取一点
上任取一点 ,连接
,连接 ,则
,则 .
.
 ,
,
 把供水站建在乙村的
把供水站建在乙村的 点处,管道沿
点处,管道沿 线路铺设的长度之和最小.
线路铺设的长度之和最小.
 即最小值为
即最小值为 .··········· (7分)
.··········· (7分)
方案三:作点 关于射线
关于射线 的对称点
的对称点 ,连接
,连接 ,则
,则 .
.
作 于点
于点 ,交
,交 于点
于点 ,交
,交 于点
于点 ,
,
 为点
为点 到
到 的最短距离,即
的最短距离,即 .
.
在 中,
中, ,
, ,
,
 .
. .
.
 ,
, 两点重合,即
两点重合,即 过
过 点.
点.
在 中,
中, ,
, .············································· (10分)
.············································· (10分)
在线段 上任取一点
上任取一点 ,过
,过 作
作 于点
于点 ,连接
,连接 .
.
显然 .
.
 把供水站建在甲村的
把供水站建在甲村的 处,管道沿
处,管道沿 线路铺设的长度之和最小.
线路铺设的长度之和最小.
即最小值为 .································································ (11分)
.································································ (11分)
综上, ,
, 供水站建在
供水站建在 处,所需铺设的管道长度最短.········ (12分)
处,所需铺设的管道长度最短.········ (12分)
25. 解:(1)取 中点
中点 ,联结
,联结 ,
,
 为
为 的中点,
的中点, ,
, .································· (1分)
.································· (1分)
又 ,
, .··········································································· (1分)
.··········································································· (1分)
 ,得
,得 ;······································ (2分)(1分)
;······································ (2分)(1分)
(2)由已知得 .··································································· (1分)
.··································································· (1分)
 以线段
以线段 为直径的圆与以线段
为直径的圆与以线段 为直径的圆外切,
为直径的圆外切,
 ,即
,即 .·························· (2分)
.·························· (2分)
解得 ,即线段
,即线段 的长为
的长为 ;······································································· (1分)
;······································································· (1分)
(3)由已知,以 为顶点的三角形与
为顶点的三角形与 相似,
相似,
又易证得 .··············································································· (1分)
.··············································································· (1分)
由此可知,另一对对应角相等有两种情况:① ;②
;② .
.
①当 时,
时,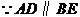 ,
, .
. .
.
 ,易得
,易得 .得
.得 ;······················································· (2分)
;······················································· (2分)
②当 时,
时,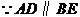 ,
, .
.
 .又
.又 ,
, .
.
 ,即
,即 ,得
,得 .
.
解得 ,
, (舍去).即线段
(舍去).即线段 的长为2.········································ (2分)
的长为2.········································ (2分)
综上所述,所求线段 的长为8或2.
的长为8或2.
24. 解:(1)∵点 在
在 上,
上,
∴ ,
,
∴ ,
,
∴ .
.
(2)连结 , 由题意易知
, 由题意易知 ,
,
∴ .
.
(3)正方形AEFG在绕A点旋转的过程中,F点的轨迹是以点A为圆心,AF为半径的圆.
第一种情况:当b>2a时,存在最大值及最小值;
因为 的边
的边 ,故当F点到BD的距离取得最大、最小值时,
,故当F点到BD的距离取得最大、最小值时, 取得最大、最小值.
取得最大、最小值.
如图②所示 时,
时,
 的最大值=
的最大值=
 的最小值=
的最小值=
第二种情况:当b=2a时,存在最大值,不存在最小值;
 的最大值=
的最大值= .(如果答案为4a2或b2也可)
.(如果答案为4a2或b2也可)

23. 解(Ⅰ)当 ,
, 时,抛物线为
时,抛物线为 ,
,
方程 的两个根为
的两个根为 ,
, .
.
∴该抛物线与 轴公共点的坐标是
轴公共点的坐标是 和
和 . ················································ 2分
. ················································ 2分
(Ⅱ)当 时,抛物线为
时,抛物线为 ,且与
,且与 轴有公共点.
轴有公共点.
对于方程 ,判别式
,判别式 ≥0,有
≥0,有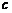 ≤
≤ . ········································ 3分
. ········································ 3分
①当 时,由方程
时,由方程 ,解得
,解得 .
.
此时抛物线为 与
与 轴只有一个公共点
轴只有一个公共点 .·································
4分
.·································
4分
②当 时,
时,
 时,
时,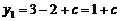 ,
,
 时,
时, .
.
由已知 时,该抛物线与
时,该抛物线与 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为 ,
,
应有 即
即
解得 .
.
综上, 或
或 . ················································································ 6分
. ················································································ 6分
(Ⅲ)对于二次函数 ,
,
由已知 时,
时, ;
; 时,
时, ,
,
又 ,∴
,∴ .
.
于是 .而
.而 ,∴
,∴ ,即
,即 .
.
∴ . ············································································································ 7分
. ············································································································ 7分
∵关于 的一元二次方程
的一元二次方程 的判别式
的判别式
 ,
,
 ∴抛物线
∴抛物线 与
与 轴有两个公共点,顶点在
轴有两个公共点,顶点在 轴下方.····························· 8分
轴下方.····························· 8分
又该抛物线的对称轴 ,
,
由 ,
, ,
, ,
,
得 ,
,
∴ .
.
又由已知 时,
时, ;
; 时,
时, ,观察图象,
,观察图象,
可知在 范围内,该抛物线与
范围内,该抛物线与 轴有两个公共点. ············································ 10分
轴有两个公共点. ············································ 10分
22. 解:( 1)由已知得:
 解得
解得
c=3,b=2
 ∴抛物线的线的解析式为
∴抛物线的线的解析式为
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,所以E(3,0)
设对称轴与x轴的交点为F
所以四边形ABDE的面积=
=
=
=9
(3)相似
如图,BD=
BE=
DE=
所以 ,
,  即:
即:  ,所以
,所以 是直角三角形
是直角三角形
所以 ,且
,且 ,
,
所以 .
.
21.解:
(1)m=-5,n=-3
(2)y= x+2
x+2
(3)是定值.
因为点D为∠ACB的平分线,所以可设点D到边AC,BC的距离均为h,
设△ABC AB边上的高为H,
则利用面积法可得:

(CM+CN)h=MN﹒H

又 H=
化简可得 (CM+CN)﹒
故 
20. 解:(1)如图,过点B作BD⊥OA于点D.
在Rt△ABD中,
∵∣AB∣= ,sin∠OAB=
,sin∠OAB= ,
,
∴∣BD∣=∣AB∣·sin∠OAB
= ×
× =3.
=3.
又由勾股定理,得


∴∣OD∣=∣OA∣-∣AD∣=10-6=4.
∵点B在第一象限,∴点B的坐标为(4,3). ……3分
设经过O(0,0)、C(4,-3)、A(10,0)三点的抛物线的函数表达式为
y=ax2+bx(a≠0).
由
∴经过O、C、A三点的抛物线的函数表达式为 ……2分
……2分
(2)假设在(1)中的抛物线上存在点P,使以P、O、C、A为顶点的四边形为梯形
①∵点C(4,-3)不是抛物线 的顶点,
的顶点,
∴过点C做直线OA的平行线与抛物线交于点P1 .
则直线CP1的函数表达式为y=-3.
对于 ,令y=-3
,令y=-3 x=4或x=6.
x=4或x=6.
∴
而点C(4,-3),∴P1(6,-3).
在四边形P1AOC中,CP1∥OA,显然∣CP1∣≠∣OA∣.
∴点P1(6,-3)是符合要求的点. ……1分
②若AP2∥CO.设直线CO的函数表达式为
将点C(4,-3)代入,得
∴直线CO的函数表达式为
于是可设直线AP2的函数表达式为
将点A(10,0)代入,得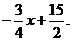
∴直线AP2的函数表达式为
由 ,即(x-10)(x+6)=0.
,即(x-10)(x+6)=0.
∴
而点A(10,0),∴P2(-6,12).
过点P2作P2E⊥x轴于点E,则∣P2E∣=12.
在Rt△AP2E中,由勾股定理,得

而∣CO∣=∣OB∣=5.
∴在四边形P2OCA中,AP2∥CO,但∣AP2∣≠∣CO∣.
∴点P2(-6,12)是符合要求的点. ……1分
③若OP3∥CA,设直线CA的函数表达式为y=k2x+b2
将点A(10,0)、C(4,-3)代入,得

∴直线CA的函数表达式为
∴直线OP3的函数表达式为
由 即x(x-14)=0.
即x(x-14)=0.
∴
而点O(0,0),∴P3(14,7).
过点P3作P3E⊥x轴于点E,则∣P3E∣=7.
在Rt△OP3E中,由勾股定理,得

而∣CA∣=∣AB∣= .
.
∴在四边形P3OCA中,OP3∥CA,但∣OP3∣≠∣CA∣.
∴点P3(14,7)是符合要求的点. ……1分
综上可知,在(1)中的抛物线上存在点P1(6,-3)、P2(-6,12)、P3(14,7),
使以P、O、C、A为顶点的四边形为梯形. ……1分
(3)由题知,抛物线的开口可能向上,也可能向下.
①当抛物线开口向上时,则此抛物线与y轴的副半轴交与点N.
 可设抛物线的函数表达式为
可设抛物线的函数表达式为 (a>0).
(a>0).
即

如图,过点M作MG⊥x轴于点G.
∵Q(-2k,0)、R(5k,0)、G( 、N(0,-10ak2)、M
、N(0,-10ak2)、M
∴





∴ ……2分
……2分
②当抛物线开口向下时,则此抛物线与y轴的正半轴交于点N,
同理,可得 ……1分
……1分
综上所知, 的值为3:20.
……1分
的值为3:20.
……1分
19. 解:(1)在 中,令
中,令


 ,
,
 ,
, ····················································· 1分
····················································· 1分
又 点
点 在
在 上
上


 的解析式为
的解析式为 ···················································································· 2分
···················································································· 2分
(2)由 ,得
,得
 ·························································· 4分
·························································· 4分
 ,
,
 ,
, ····································································································· 5分
····································································································· 5分
 ······························································································· 6分
······························································································· 6分
(3)过点 作
作 于点
于点


 ····································································································· 7分
····································································································· 7分
 ················································································································ 8分
················································································································ 8分
由直线 可得:
可得:
 在
在 中,
中, ,
, ,则
,则
 ,
, ····························································································· 9分
····························································································· 9分

 ·························································································· 10分
·························································································· 10分
 ··································································································· 11分
··································································································· 11分
 此抛物线开口向下,
此抛物线开口向下, 当
当 时,
时,
 当点
当点 运动2秒时,
运动2秒时, 的面积达到最大,最大为
的面积达到最大,最大为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com