
2. 用适量的原料经玻璃熔炉反应后制取的普通玻璃中,含钠9.6%,含钙8.4%,含硅35.1%。习惯上可用下列哪个化学式来表示该玻璃的组成( )
A.Na2O·CaO·SiO2 B.2Na·CaO·6SiO2
C.Na2O·CaO·6SiO2 D.Na2O·CaO·5SiO2
1.1985年,科学家发现了一种新的单质碳系列-碳笼,其中最丰富的是C60。根据其结构特点,科学家称之为“足球烯”,这是一种分子晶体。据此推测下列说法中不正确的是( )
A.金刚石、石墨、足球烯都是碳的同素异形体 B.一定条件下,足球烯可发生加成反应
C.石墨、足球烯均可作为高温条件下的润滑材料
D.足球烯在苯中的溶解度比在酒精中的溶解度大
1 若tanAtanB=tanA+tanB+1,则cos(A+B)的值为( )
若tanAtanB=tanA+tanB+1,则cos(A+B)的值为( )

2 已知α+β=kπ-
已知α+β=kπ- (k∈Z)则(1-tanα)(1-tanβ)的值为( )
(k∈Z)则(1-tanα)(1-tanβ)的值为( )
A -1 B
-1 B 1 C
1 C -2 D
-2 D 2
2
3 若a=tan100°,b=tan25°,c=tan55°,则a、b、c之间的关系是( )
若a=tan100°,b=tan25°,c=tan55°,则a、b、c之间的关系是( )
A a+b+c=abc
B
a+b+c=abc
B ab+bc+ca=1
ab+bc+ca=1
C ab+bc+ca=a+b+c
D
ab+bc+ca=a+b+c
D ab+bc+ca=a2+b2+c2
ab+bc+ca=a2+b2+c2
4 tan10°+tan35°+tan10°tan35°=
tan10°+tan35°+tan10°tan35°=

5
 =
=

6 (1+tan1°)(1+tan2°)(1+tan3°)……(1+tan44°)(1+tan45°)=
(1+tan1°)(1+tan2°)(1+tan3°)……(1+tan44°)(1+tan45°)= 
例1 在斜三角形△ABC中,求证:tanA+tanB+tanC=tanA•tanB•tanC
证一:在△ABC中,∵A+B+C=p ∴A+B=p-C
从而有 tan(A+B)=tan(p-C) 即:
∴tanA+tanB=-tanC+tanAtanBtanC
即:tanA+tanB+tanC=tanA•tanB•tanC
证二:左边= tan(A+B)(1-tanAtanB) +tanC=tan(p-C) (1-tanAtanB) +tanC
=-tanC+ tanAtanBtanC+tanC=tanAtanBtanC=右边
例2 求(1+tan1°)(1+tan2°)(1+tan3°)……(1+tan44°)
解: (1+tan1°)(1+tan44°)=1+tan1°+tan44°+tan1°tan44°
=1+tan45°(1- tan1°tan44°)+ tan1°tan44°=2
同理:(1+tan2°)(1+tan43°)=2 (1+tan3°)(1+tan42°)=2 ……
∴原式=222
例3 已知tanq和 是方程
是方程 的两个根,
的两个根,
证明:p-q+1=0
证:由韦达定理:tanq+ =-p ,tanq•
=-p ,tanq• =q
=q
∴
∴p-q+1=0
例4 已知tana= ,tan(-b)=
,tan(-b)= (tanatanb+m),又a,b都是钝角,求a+b的值
(tanatanb+m),又a,b都是钝角,求a+b的值
解:∵两式作差,得:tana+tanb= (1-tanatanb)
(1-tanatanb)
即  ∴
∴
又 a,b都是钝角 ∴p<a+b<2p ∴a+b
例5 已知tana,tanb是关于x的一元二次方程x2+px+2=0的两实根,求 的值
的值
解:∵

tana,tanb是方程x2+px+2=0的两实根
∴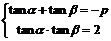 ∴
∴
例6 求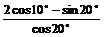 的值
的值
解:原式=

=
1.两角和与差的正、余弦公式






20、过点P(2,1)作直线l分别交x、y轴正半轴于A,B两点.
(1)当ΔAOB面积为 时,求直线l的方程;x+y-3=0或x+4y-6=0
时,求直线l的方程;x+y-3=0或x+4y-6=0
(2)当ΔAOB面积最小时,求直线l的方程. x+2y-4=0
解:(1)
由题意可设直线l的方程为 (a>0,b>0)
(a>0,b>0)
由已知可得 解得
解得 或
或
所以直线l的方程为x+y-3=0或x+4y-6=0
(2) 由题意可设直线l的方程为 (a>0,b>0)
(a>0,b>0)
因为直线l过点P(2,1),所以有
因为a>0,b>0,所以

即ab ,当且仅当
,当且仅当 即a=4,b=2时取“=”
即a=4,b=2时取“=”
此时SΔAOB取得最小值4,
直线l的方程为x+2y-4=0。
19、 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AD=a,E是PD的中点。
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AD=a,E是PD的中点。
(1)求证:PB∥平面AEC;
(2)求证:平面PDC⊥平面AEC;
(3)求点B到平面PDC的距离。 a
a
证明(1)连结BD交AC于0连结OE,可证得OE∥PB,故PB∥平面AEC
(2) PA⊥平面ABCD,
PA⊥平面ABCD, PA⊥CD,
PA⊥CD,
 底面是正方形,
底面是正方形, AD⊥CD
AD⊥CD
 CD⊥平面PAD
CD⊥平面PAD
 CD⊥AE
CD⊥AE
又 PA=AD,E是PD的中点,
PA=AD,E是PD的中点,
 AE⊥PD
AE⊥PD
 AE⊥平面PDC,故平面PDC⊥平面AEC
AE⊥平面PDC,故平面PDC⊥平面AEC
解(3) 底面是正方形
底面是正方形
 AB∥CD,
AB∥CD, AB∥平面PDC
AB∥平面PDC
 点B到平面PDC的距离即为点A到平面PDC的距离,
点B到平面PDC的距离即为点A到平面PDC的距离,
由(2)知AE⊥平面PDC
所以AE为点B到平面PDC的距离,
 PA⊥平面ABCD,
PA⊥平面ABCD, PA⊥AD,
PA⊥AD,
在RtΔPAD中,PA=AD,E是PD的中点,
所以AE= a,
a,
故点B到平面PDC的距离为 a。
a。
18、已知直线 :
:
 .
.
(1)若直线 的倾斜角为锐角,求m的取值范围;
的倾斜角为锐角,求m的取值范围;
(2)求证:不论m为何值时,直线 必过某一定点,并求出定点的坐标。(9,-4)
必过某一定点,并求出定点的坐标。(9,-4)
解:(1)因为直线 的倾斜角为锐角,
的倾斜角为锐角,
所以直线 的斜率k>0
的斜率k>0
又直线 的方程
的方程
 ,
,
所以k= 即
即 >0,解得
>0,解得 <m<1
<m<1
(2)直线 的方程
的方程
 可化为
可化为
(x+2y-1)m-x-y+5=0
不论m为何值时,直线 过定点即为直线x+2y-1=0与直线-x-y+5=0的交点。
过定点即为直线x+2y-1=0与直线-x-y+5=0的交点。
解方程组可得定点为(9,-4)。
17、已知直线 :
: x-y+1=0,直线
x-y+1=0,直线 经过点A(1,2),求满足下列条件的直线
经过点A(1,2),求满足下列条件的直线 的方程。
的方程。
(1)直线 的倾斜角是直线
的倾斜角是直线 的倾斜角的2倍;
的倾斜角的2倍;
(2)直线 的倾斜角正弦值为
的倾斜角正弦值为 。3x-4y+5=0或3x+4y-11=0
。3x-4y+5=0或3x+4y-11=0
解(1)因为直线 的方程为
的方程为 x-y+1=0,
x-y+1=0,
所以直线 的斜率为
的斜率为 ,倾斜角的600
,倾斜角的600
故直线 的倾斜角为1200,斜率为-
的倾斜角为1200,斜率为-
又直线 经过点A(1,2)
经过点A(1,2)
所以 方程为y-2=-
方程为y-2=- (x-1)即为
(x-1)即为 x+y-2-
x+y-2- =0
=0
(2)设直线 的倾斜角为
的倾斜角为 ,则sin
,则sin =
=
因为 ∈
∈ ,所以cos
,所以cos =±
=± ,tan
,tan =±
=±
直线 经过点A(1,2)
经过点A(1,2)
故 方程为3x-4y+5=0或3x+4y-11=0。
方程为3x-4y+5=0或3x+4y-11=0。
16、已知PA⊥平面ABC, AB是⊙O的直径, C是⊙O上的任一点. 求证: BC⊥PC .

简证: PA⊥平面ABC
PA⊥平面ABC
 PA⊥BC
PA⊥BC
又 AB是⊙O的直径, C是⊙O上的任一点
AB是⊙O的直径, C是⊙O上的任一点
 AC⊥BC
AC⊥BC
 BC⊥平面PAC
BC⊥平面PAC
故BC⊥PC。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com