
18. 解:(1)点 在
在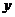 轴上························································································· 1分
轴上························································································· 1分
理由如下:
连接 ,如图所示,在
,如图所示,在 中,
中, ,
, ,
,
 ,
,
由题意可知:

 点
点 在
在 轴上,
轴上, 点
点 在
在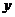 轴上.············································································ 3分
轴上.············································································ 3分
(2)过点 作
作 轴于点
轴于点
 ,
,
 在
在 中,
中, ,
,
 点
点 在第一象限,
在第一象限,
 点
点 的坐标为
的坐标为 ····························································································· 5分
····························································································· 5分
由(1)知 ,点
,点 在
在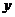 轴的正半轴上
轴的正半轴上
 点
点 的坐标为
的坐标为
 点
点 的坐标为
的坐标为 ······························································································· 6分
······························································································· 6分
 抛物线
抛物线 经过点
经过点 ,
,
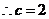
由题意,将 ,
, 代入
代入 中得
中得
 解得
解得
 所求抛物线表达式为:
所求抛物线表达式为: ·························································· 9分
·························································· 9分
(3)存在符合条件的点 ,点
,点 .············································································ 10分
.············································································ 10分
理由如下: 矩形
矩形 的面积
的面积
 以
以 为顶点的平行四边形面积为
为顶点的平行四边形面积为 .
.
由题意可知 为此平行四边形一边,
为此平行四边形一边,
又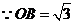
 边上的高为2······································································································ 11分
边上的高为2······································································································ 11分
依题意设点 的坐标为
的坐标为
 点
点 在抛物线
在抛物线 上
上

解得, ,
,
 ,
,
 以
以 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
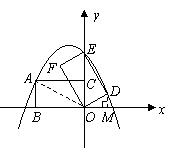
 ,
, ,
,
 当点
当点 的坐标为
的坐标为 时,
时,
点 的坐标分别为
的坐标分别为 ,
, ;
;
当点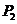 的坐标为
的坐标为 时,
时,
点 的坐标分别为
的坐标分别为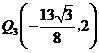 ,
, .·················································· 14分
.·················································· 14分
(以上答案仅供参考,如有其它做法,可参照给分)
17. 解:(1) 直线
直线 与
与 轴交于点
轴交于点 ,与
,与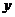 轴交于点
轴交于点 .
.
 ,
,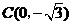 ······························································································· 1分
······························································································· 1分
 点
点 都在抛物线上,
都在抛物线上,


 抛物线的解析式为
抛物线的解析式为 ······························································ 3分
······························································ 3分
 顶点
顶点 ····································································································· 4分
····································································································· 4分
(2)存在····················································································································· 5分
 ··················································································································· 7分
··················································································································· 7分
 ·················································································································· 9分
·················································································································· 9分
(3)存在···················································································································· 10分
理由:
解法一:
延长 到点
到点 ,使
,使 ,连接
,连接 交直线
交直线 于点
于点 ,则点
,则点 就是所求的点.
就是所求的点.
··························································································· 11分
 过点
过点 作
作 于点
于点 .
.
 点在抛物线
点在抛物线 上,
上,
在 中,
中, ,
,
 ,
, ,
,
在 中,
中, ,
,
 ,
, ,
, ····················································· 12分
····················································· 12分
设直线 的解析式为
的解析式为
 解得
解得
 ······································································································ 13分
······································································································ 13分
 解得
解得

 在直线
在直线 上存在点
上存在点 ,使得
,使得 的周长最小,此时
的周长最小,此时 .········· 14分
.········· 14分
解法二:
 过点
过点 作
作 的垂线交
的垂线交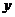 轴于点
轴于点 ,则点
,则点 为点
为点 关于直线
关于直线 的对称点.连接
的对称点.连接 交
交 于点
于点 ,则点
,则点 即为所求.···················································································· 11分
即为所求.···················································································· 11分
过点 作
作 轴于点
轴于点 ,则
,则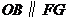 ,
, .
.
 ,
,

同方法一可求得 .
.
在 中,
中, ,
, ,可求得
,可求得 ,
,
 为线段
为线段 的垂直平分线,可证得
的垂直平分线,可证得 为等边三角形,
为等边三角形,
 垂直平分
垂直平分 .
.
即点 为点
为点 关于
关于 的对称点.
的对称点. ··················································· 12分
··················································· 12分
设直线 的解析式为
的解析式为 ,由题意得
,由题意得
 解得
解得
 ······································································································ 13分
······································································································ 13分
 解得
解得

 在直线
在直线 上存在点
上存在点 ,使得
,使得 的周长最小,此时
的周长最小,此时 . 1
. 1
16.
解:(1) ,
, .
.


(2)当 时,过
时,过 点作
点作 ,交
,交 于
于 ,如图1,
,如图1,
则 ,
, ,
,
 ,
, .
.
(3)① 能与
能与 平行.
平行.
若 ,如图2,则
,如图2,则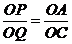 ,
,
即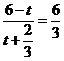 ,
, ,而
,而 ,
,
 .
.
② 不能与
不能与 垂直.
垂直.
若 ,延长
,延长 交
交 于
于 ,如图3,
,如图3,
则 .
.
 .
.
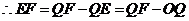

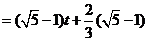 .
.
又 ,
, ,
,
 ,
,
 ,而
,而 ,
,
 不存在.
不存在.
15. 解:(1)解法1:根据题意可得:A(-1,0),B(3,0);
则设抛物线的解析式为 (a≠0)
(a≠0)
又点D(0,-3)在抛物线上,∴a(0+1)(0-3)=-3,解之得:a=1
∴y=x2-2x-3···································································································· 3分
自变量范围:-1≤x≤3···················································································· 4分
解法2:设抛物线的解析式为 (a≠0)
(a≠0)
根据题意可知,A(-1,0),B(3,0),D(0,-3)三点都在抛物线上
∴ ,解之得:
,解之得:
∴y=x2-2x-3··············································································· 3分
自变量范围:-1≤x≤3······························································ 4分
(2)设经过点C“蛋圆”的切线CE交x轴于点E,连结CM,
在Rt△MOC中,∵OM=1,CM=2,∴∠CMO=60°,OC=
在Rt△MCE中,∵OC=2,∠CMO=60°,∴ME=4
∴点C、E的坐标分别为(0, ),(-3,0) ·················································· 6分
),(-3,0) ·················································· 6分
 ∴切线CE的解析式为
∴切线CE的解析式为 ··························································· 8分
··························································· 8分
(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0) ·························· 9分
由题意可知方程组 只有一组解
只有一组解
即 有两个相等实根,∴k=-2············································· 11分
有两个相等实根,∴k=-2············································· 11分
∴过点D“蛋圆”切线的解析式y=-2x-3····················································· 12分
14.  解:(1)由题意可知,
解:(1)由题意可知, .
.
解,得 m=3. ………………………………3分
∴ A(3,4),B(6,2);
∴ k=4×3=12. ……………………………4分
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴
上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵ 四边形AN1M1B为平行四边形,
∴ 线段N1M1可看作由线段AB向左平移3个单位,
再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴ N1点坐标为(0,4-2),即N1(0,2); ………………………………5分
M1点坐标为(6-3,0),即M1(3,0). ………………………………6分
设直线M1N1的函数表达式为 ,把x=3,y=0代入,解得
,把x=3,y=0代入,解得 .
.
∴ 直线M1N1的函数表达式为 . ……………………………………8分
. ……………………………………8分
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵ AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴ N1M1∥M2N2,N1M1=M2N2.
∴ 线段M2N2与线段N1M1关于原点O成中心对称.
∴ M2点坐标为(-3,0),N2点坐标为(0,-2). ………………………9分
设直线M2N2的函数表达式为 ,把x=-3,y=0代入,解得
,把x=-3,y=0代入,解得 ,
,
∴ 直线M2N2的函数表达式为 .
.
所以,直线MN的函数表达式为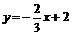 或
或 . ………………11分
. ………………11分
(3)选做题:(9,2),(4,5). ………………………………………………2分
13. 解:(1)分别过D,C两点作DG⊥AB于点G,CH⊥AB于点H. ……………1分
∵ AB∥CD,
∴ DG=CH,DG∥CH.
∴ 四边形DGHC为矩形,GH=CD=1.
 ∵ DG=CH,AD=BC,∠AGD=∠BHC=90°,
∵ DG=CH,AD=BC,∠AGD=∠BHC=90°,
∴ △AGD≌△BHC(HL).
∴ AG=BH= =3. ………2分
=3. ………2分
∵ 在Rt△AGD中,AG=3,AD=5,
∴ DG=4.
∴  . ………………………………………………3分
. ………………………………………………3分
 (2)∵ MN∥AB,ME⊥AB,NF⊥AB,
(2)∵ MN∥AB,ME⊥AB,NF⊥AB,
∴ ME=NF,ME∥NF.
∴ 四边形MEFN为矩形.
∵ AB∥CD,AD=BC,
∴ ∠A=∠B.
∵ ME=NF,∠MEA=∠NFB=90°,
∴ △MEA≌△NFB(AAS).
∴ AE=BF. ……………………4分
设AE=x,则EF=7-2x. ……………5分
∵ ∠A=∠A,∠MEA=∠DGA=90°,
∴ △MEA∽△DGA.
∴  .
.
∴ ME= .
…………………………………………………………6分
.
…………………………………………………………6分
∴  . ……………………8分
. ……………………8分
当x= 时,ME=
时,ME= <4,∴四边形MEFN面积的最大值为
<4,∴四边形MEFN面积的最大值为 .……………9分
.……………9分
(3)能. ……………………………………………………………………10分
由(2)可知,设AE=x,则EF=7-2x,ME= .
.
若四边形MEFN为正方形,则ME=EF.
即  7-2x.解,得
7-2x.解,得 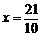 . ……………………………………………11分
. ……………………………………………11分
∴ EF= <4.
<4.
∴ 四边形MEFN能为正方形,其面积为 .
.
12. 解:(1) .····················································································· 3分
.····················································································· 3分
(2)相等,比值为 .················· 5分(无“相等”不扣分有“相等”,比值错给1分)
.················· 5分(无“相等”不扣分有“相等”,比值错给1分)
(3)设 ,
,
在矩形 中,
中, ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .···································································································· 6分
.···································································································· 6分
同理 .
.
 ,
,
 ,
,
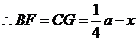 .······························································································· 7分
.······························································································· 7分
 ,
,
 ,······························································································ 8分
,······························································································ 8分
解得 .
.
即 .······································································································ 9分
.······································································································ 9分
(4) ,·············································································································· 10分
,·············································································································· 10分
 . 12分
. 12分
11. 解:(1)设 地经杭州湾跨海大桥到宁波港的路程为
地经杭州湾跨海大桥到宁波港的路程为 千米,
千米,
由题意得 ,································································································ 2分
,································································································ 2分
解得 .
.
 地经杭州湾跨海大桥到宁波港的路程为180千米.················································· 4分
地经杭州湾跨海大桥到宁波港的路程为180千米.················································· 4分
(2) (元),
(元),
 该车货物从
该车货物从 地经杭州湾跨海大桥到宁波港的运输费用为380元.···························· 6分
地经杭州湾跨海大桥到宁波港的运输费用为380元.···························· 6分
(3)设这批货物有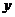 车,
车,
由题意得 ,···························································· 8分
,···························································· 8分
整理得 ,
,
解得 ,
, (不合题意,舍去),································································ 9分
(不合题意,舍去),································································ 9分
 这批货物有8车.···································································································· 10分
这批货物有8车.···································································································· 10分
10.




9.



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com