3．要合理分配时间，每道题都要做答，不要空题。要镇静作答，每一道题都能有自己的得分点。

选择题

2．答题卡设计的空白应能满足答案所需，请提醒学生不要字迹太潦草、太大，以

至于所留空白不够填写。

1．一定在题号的指定范围内作答案，答题框线以外及背面的答案无效。有注释也不行。

25、(01上海卷)(10分)如图A所示，一质量为m的物体系于长度分别为l₁、l₂的两根细线上，l₁的一端悬挂在天花板上，与竖直方向夹角为θ，l₂水平拉直，物体处于平衡状态。现将l₂线剪断，求剪断瞬时物体的加速度。

(l)下面是某同学对该题的一种解法：

解：设l₁线上拉力为T₁，线上拉力为T_2，重力为mg，物体在三力作用下保持平衡

T₁cosθ＝mg，　 T₁sinθ＝T₂，　 T₂＝mgtgθ

剪断线的瞬间，T₂突然消失，物体即在T₂反方向获得加速度。因为mg tgθ＝ma，所以加速度a＝g tgθ，方向在T₂反方向。

你认为这个结果正确吗？请对该解法作出评价并说明理由。

(2)若将图A中的细线l₁改为长度相同、质量不计的轻弹簧，如图B所示，其他条件不变，求解的步骤和结果与(l)完全相同，即 a＝g tgθ，你认为这个结果正确吗？请说明理由。

解：(1)错。

因为I₂被剪断的瞬间，l₁上的张力大小发生了变化。

(2)对。

因为G被剪断的瞬间，弹簧U的长度末及发生变化，乃大小和方向都不变。

评分标准：全题10分。第(1)小题6分，第(2)小题4分。其中

(1)结论正确，得3分；评价和说明理由正确，得3分。

(2)结论正确，得2分；评价和说明理由正确，得2分。

24、(00天津、江西卷)(13分)图中是用电动砂轮打磨工件的装置，砂轮的转轴过图中O点垂直于纸面，AB是一长度，质量的均匀刚性细杆，可绕过A端的固定轴在竖直面(图中纸面)内无摩擦地转动，工件C固定在AB杆上，其质量，工件的重心、工件与砂轮的接触点P以及O点都在过AB中点的竖直线上，P到AB杆的垂直距离，AB杆始终处于水平位置，砂轮与工件之间的动摩擦因数

(1)当砂轮静止时，要使工件对砂轮的压力N，则施于B端竖直向下的力应是多大？

(2)当砂轮逆时针转动时，要使工件对砂轮的压力仍为N，则施于B端竖直向下的力应是多大？

解：(1)当砂轮静止时，把AB杆和工件看成一个物体，它受到的外力对A轴的力矩有：重力的力矩()

砂轮对工件的支持力的力矩

的力矩

由力矩的平衡，得

　　　 　　　　　　　　　　　　　1

解得

　　　　　　　　　　　　　　　　　 2

代入数据得

　　　　　　　　　　　　　　　　　　　　　　　　 3

(2)当砂轮转动时，除重力、支持力和的力矩外，还有砂轮作用于工件的摩擦力的力矩。

由力矩的平平衡；得

　　　　　　　　　 4

解得

　　　　　　　　　　　　 5

代入数据得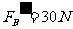　

23、(07宁夏理综 )(物理--选修2－2)

　 塔式起重机的结构如图所示，设机架重P＝400 kN，悬臂长度为L＝10 m，平衡块重W＝200 kN，平衡块与中心线OO^/的距离可在1 m到6 m间变化，轨道A、B间的距离为4 m。

　 ⑴当平衡块离中心线1 m，右侧轨道对轮子的作用力f_B是左侧轨道对轮子作用力f_A的2倍，问机架重心离中心线的距离是多少？

　 ⑵当起重机挂钩在离中心线OO^/10 m处吊起重为G＝100 kN的重物时，平衡块离OO^/的距离为6 m，问此时轨道B对轮子的作用力F_B时多少？

、解：⑴空载时合力为零：

　　　　　　　　　 已知：f_B＝2f_A

　　　　　　　　　 求得：f_A＝200 kN

　　　　　　　　　　　　 f_B＝400 kN

　　　　 设机架重心在中心线右侧，离中心线的距离为x，以A为转轴，力矩平衡

　　　　　　　 求得：x＝1.5 m

　　　 ⑵以A为转轴，力矩平衡

　　　　　　　 求得：F_B＝450 kN

33.[物理--选修2-2](2)(10分)液压千斤顶是利用密闭容器内的液体能够把液体所受到的压强行各个方向传递的原理制成的。图为一小型千斤顶的结构示意图。大活塞的直径D₁=20cm，小活塞B的直径D₂=5cm，手柄的长度OC=50cm，小活塞与手柄的连接点到转轴O的距离OD=10cm。现用此千斤顶使质量m=4×10³kg的重物升高了h=10cm。g取10m/s²，求

(i)若此千斤顶的效率为80%，在这一过程中人做的功为多少？

(ii)若此千斤顶的效率为100%，当重物上升时，人对手柄的作用力F至少要多大？

解析：

(i)将重物托起h需要做的功

　　　　　 　　　　　　　　　　　　①

设人对手柄做的功为，则千斤顶的效率为

　　　　　　　　　　　　 　②

代入数据可得

　　　　 　　　　　　　　　　③

　 (i i)设大活塞的面积为, 小活塞的面积为，作用在小活塞上的压力为,当于斤顶的效率为100%时，有

　　　　　　　　　　　　 　④

　　　　　　　　　　　　 　⑤

当和F都与杠杆垂直时，手对杠杆的压力最小。利用杠杆原理，有

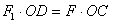　　　 　　　　　　　　　　　　⑥

由④⑤⑥式得

　　　 F=500N　　　　　　　　　　　　　 　　　　⑦

23．(09年上海物理)(12分)如图，质量均为m的两个小球A、B固定在弯成120°角的绝缘轻杆两端，OA和OB的长度均为l，可绕过O点且与纸面垂直的水平轴无摩擦转动，空气阻力不计。设A球带正电，B球带负电，电量均为q，处在竖直向下的匀强电场中。开始时，杆OB与竖直方向的夹角q₀＝60°，由静止释放，摆动到q＝90°的位置时，系统处于平衡状态，求：

(1)匀强电场的场强大小E；

(2)系统由初位置运动到平衡位置，重力做的功W_g和静电力做的功W_e；

(3)B球在摆动到平衡位置时速度的大小v。

解析：(1)力矩平衡时：(mg－qE)lsin90°＝(mg+qE)lsin(120°－90°)，

即mg－qE＝2(1)(mg+qE)，得：E＝3q(mg)；

(2)重力做功：W_g＝mgl(cos30°－cos60°)－mglcos60°＝(,2)－1)mgl，

静电力做功：W_e＝qEl(cos30°－cos60°)+qElcos60°＝,6)mgl，

(3)小球动能改变量DE_k=mv²＝W_g+W_e＝(,3)－1)mgl，

得小球的速度：v＝Dm(Ek))＝,3)－1)gl)。

22．(09年安徽卷)(14分)在2008年北京残奥会开幕式上，运动员手拉绳索向上攀登，最终点燃了主火炬，体现了残疾运动员坚忍不拔的意志和自强不息的精神。为了探究上升过程中运动员与绳索和吊椅间的作用，可将过程简化。一根不可伸缩的轻绳跨过轻质的定滑轮，一端挂一吊椅，另一端被坐在吊椅上的运动员拉住，如图所示。设运动员的质量为65kg，吊椅的质量为15kg，不计定滑轮与绳子间的摩擦。重力加速度取。当运动员与吊椅一起正以加速度上升时，试求

　 (1)运动员竖直向下拉绳的力；

　 (2)运动员对吊椅的压力。

答案：440N，275N

解析：解法一:(1)设运动员受到绳向上的拉力为F，由于跨过定滑轮的两段绳子拉力相等，吊椅受到绳的拉力也是F。对运动员和吊椅整体进行受力分析如图所示，则有：

由牛顿第三定律，运动员竖直向下拉绳的力

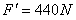
(2)设吊椅对运动员的支持力为F_N，对运动员进行受力分析如图所示，则有：

由牛顿第三定律，运动员对吊椅的压力也为275N

解法二:设运动员和吊椅的质量分别为M和m；运动员竖直向下的拉力为F，对吊椅的压力大小为F_N。

根据牛顿第三定律，绳对运动员的拉力大小为F，吊椅对运动员的支持力为F_N。分别以运动员和吊椅为研究对象，根据牛顿第二定律

　　　　　　 　　　　　　　　　　　　①

　　　　　　　　　　　　　　　　　　 ②

由①②得　　　

24．(09年山东卷)(15分)如图所示，某货场而将质量为m₁=100 kg的货物(可视为质点)从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物中轨道顶端无初速滑下，轨道半径R=1.8 m。地面上紧靠轨道次排放两声完全相同的木板A、B，长度均为l=2m，质量均为m₂=100 kg，木板上表面与轨道末端相切。货物与木板间的动摩擦因数为₁，木板与地面间的动摩擦因数=0.2。(最大静摩擦力与滑动摩擦力大小相等，取g=10 m/s²)

(1)求货物到达圆轨道末端时对轨道的压力。

(2)若货物滑上木板4时，木板不动，而滑上木板B时，木板B开始滑动，求_1-应满足的条件。

(3)若₁=0。5，求货物滑到木板A末端时的速度和在木板A上运动的时间。

解析：(1)设货物滑到圆轨道末端是的速度为，对货物的下滑过程中根据机械能守恒定律得，①

设货物在轨道末端所受支持力的大小为,根据牛顿第二定律得，②

联立以上两式代入数据得③

根据牛顿第三定律，货物到达圆轨道末端时对轨道的压力大小为3000N，方向竖直向下。

(2)若滑上木板A时，木板不动，由受力分析得④

若滑上木板B时，木板B开始滑动，由受力分析得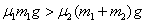⑤

联立④⑤式代入数据得⑥。

(3)，由⑥式可知，货物在木板A上滑动时，木板不动。设货物在木板A上做减速运动时的加速度大小为，由牛顿第二定律得⑦

设货物滑到木板A末端是的速度为，由运动学公式得⑧

联立①⑦⑧式代入数据得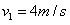⑨

设在木板A上运动的时间为t，由运动学公式得⑩

联立①⑦⑨⑩式代入数据得。

考点：机械能守恒定律、牛顿第二定律、运动学方程、受力分析