
12.已知tan( +
+ )=-
)=-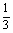 ,tan(
,tan( +
+ )=
)= .
.
(1)求tan( +
+ )的值;(2)求tan
)的值;(2)求tan 的值.
的值.
解 (1)∵tan( +
+ )=-
)=-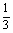 ,∴tan
,∴tan =-
=-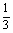 ,
,
∵tan( +
+ )=
)= =
=
=
=
= ,
,
∴tan( +
+ )=
)= =
= .
.
(2)∵tan =tan[(
=tan[( +
+ )-
)- ]=
]= ,
,
∴tan =
= =
= .
.
11.已知sin ·sin
·sin =
= ,
, ∈
∈ ,求2sin2
,求2sin2 +tan
+tan -
- -1的值.
-1的值.
解 ∵sin sin
sin =
= ,
,
∴sin cos
cos =
= ,
,
即 sin
sin =
= ,sin
,sin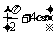 =
= ,
,
∴cos4 =
= ,又∵
,又∵ ∈
∈ ,∴4
,∴4 =
= ,
, =
= ,
,
∴2sin2 +tan
+tan -
- -1
-1
=2sin2 +
+ -
- -1=2sin2
-1=2sin2 -1+
-1+
=-cos2 +
+ =-cos
=-cos -
-
= -
- =
= .
.
10.若函数f(x)= -asin
-asin ·cos
·cos 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
解 f(x)= +asin
+asin cos
cos
= cosx+
cosx+ sinx=
sinx= sin(x+
sin(x+ ),
),
其中角 满足sin
满足sin =
= .
.
由已知,有 +
+ =4.
=4.
解之得a=±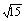 .
.
9.已知tan =
= ,tan
,tan =
=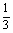 ,并且
,并且 ,
, 均为锐角,求
均为锐角,求 +2
+2 的值.
的值.
解 ∵tan =
= <1,tan
<1,tan =
=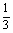 <1,
<1,
且 、
、 均为锐角,
均为锐角,
∴0< <
< ,0<
,0< <
< .
.
∴0< +2
+2 <
< .
.
又tan2 =
= =
= ,
,
∴tan( +2
+2 )=
)= =
=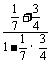 =1.
=1.
∴ +2
+2 =
= .
.
8.求值:cos4 +cos4
+cos4 +cos4
+cos4 +cos4
+cos4 =
.
=
.
答案 
7.(2008·上海理,6)函数f(x)= sinx+sin
sinx+sin 的最大值是 .
的最大值是 .
答案 2
6.若f(x)=2tanx- ,则f
,则f 的值为
.
的值为
.
答案 8
5.(cos )(cos
)(cos )=
.
)=
.
答案 
4.已知cos2 =
= (其中
(其中 ∈
∈ ),则sin
),则sin 的值为
.
的值为
.
答案 -
3.已知x∈ ,cosx=
,cosx= ,则tan2x=
.
,则tan2x=
.
答案 -
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com