
4.设f(x)=(ax+b)sinx+(cx+d)cosx,试确定常数a,b,c,d,使得f′(x)=xcosx.
解:由已知f′(x)=[(ax+b)sinx+(cx+d)cosx]′
=[(ax+b)sinx]′+[(cx+d)cosx]′
=(ax+b)′sinx+(ax+b)(sinx)′+(cx+d)′cosx+(cx+d)·(cosx)′
=asinx+(ax+b)cosx+ccosx-(cx+d)sinx
=(a-cx-d)sinx+(ax+b+c)cosx.
又∵f′(x)=xcosx,
∴必须有即
解得a=d=1,b=c=0.
|
题组二 |
导数的几何意义 |
3.(2009·安徽高考)设函数f(x)=x3+x2+tanθ,其中θ∈[0,],则导数f′(1)的取值范围是 ( )
A.[-2,2] B.[,] C.[,2] D.[,2]
解析:∵f′(x)=sinθ·x2+cosθ·x,
∴f′(1)=sinθ+cosθ=2sin(θ+).
∵θ∈[0,],∴θ+∈[,].
∴sin(θ+)∈[,1],∴f′(1)∈[,2].
答案:D
2.设f0(x)=cosx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2010(x)= ( )
A.sinx B.-sinx C.cosx D.-cosx
解析:∵f1(x)=(cosx)′=-sinx,f2(x)=(-sinx)′=-cosx,f3(x)=(-cosx)′=sinx,f4(x)=(sinx)′=cosx,…,由此可知fn(x)的值周期性重复出现,周期为4,
故f2010(x)=f2(x)=-cosx.
答案:D
1.设f(x)=xlnx,若f′(x0)=2,则x0= ( )
A.e2 B.e C. D.ln2
解析:f′(x)=x×+1×lnx=1+lnx,由1+lnx0=2,
知x0=e.
答案:B
20、在直角坐标系中,A (1,t),C(-2t,2), (O是坐标原点),其中t∈(0,+∞)。
(O是坐标原点),其中t∈(0,+∞)。
⑴求四边形OABC在第一象限部分的面积S(t);
⑵确定函数S(t)的单调区间,并求S(t)的最小值。
19、设函数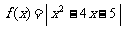 .
.
(1)在区间 上画出函数
上画出函数 的图像;
的图像;
(2)当 时,求证:在区间
时,求证:在区间 上,
上,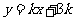 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
18、已知函数 的图象与x
的图象与x y轴分别相交于点A
y轴分别相交于点A B,
B, (
(

 分别是与x
分别是与x y轴正半轴同方向的单位向量), 函数
y轴正半轴同方向的单位向量), 函数

(1) 求k b的值;
b的值;
(2) 当x满足 时,求函数
时,求函数 的最小值
的最小值
17.(本题满分15分)
在 中,
中, 分别是角A、B、C的对边,
分别是角A、B、C的对边,

 ,且
,且 .
.
(1)求角A的大小;
(2)求 的值域.
的值域.
16、 如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
15、已知 均为非零向量,当
均为非零向量,当


 的模取最小值时,
的模取最小值时,
①求 的值;
的值;
②已知 与
与 为不共线向量,求证
为不共线向量,求证 与
与

 垂直.
垂直.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com