6.如图4所示，在同一竖直面内，小球a、b从高度不同的两点，分别以初速度v_a 和

v_b沿水平方向抛出，经过时间t_a和t_b后落到与两抛出点水平距离相等的P点．若

不计空气阻力，下列关系式正确的是　　　　　　　　　　　　　　 (　) 　　　图4

A．t_a＞t_b　　　B．v_a＞v_b

C．v_a＜v_b 　　　　　D．t_a＜t_b

解析：两小球做平抛运动，由题图可知h_a＞h_b，则t_a＞t_b；又水平位移相同，根据x＝vt

可知v_a＜v_b.

答案：AC

5.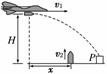如图3所示，我某集团军在一次空地联合军事演习中，离地面H高处的飞机以水平对地速度v₁发射一颗炸弹轰炸地面目标P，反应灵敏的地面拦截系统同时以初速度v₂竖直向上发射一颗炮弹拦截(炮弹运动过程看做竖直上抛)，设此时拦截系统与飞机的水平距离为x，若拦截成功，不计空气阻力，则v₁、v₂的关系应满足　　　　　　　　　　　 　　　　　　　　　　　　　　　　　(　)　　 　图3

A．v₁＝v₂ 　B．v₁＝v₂

C．v₁＝v₂ 　　　　　　　　　D．v₁＝v₂

解析：由题知从发射到拦截成功水平方向应满足：

x＝v₁t，同时竖直方向应满足：

H＝gt²+v₂t－gt²＝v₂t，

所以有＝，即v₁＝v₂，C选项正确．

答案：C

4．某同学对着墙壁练习打网球，假定球在墙面上以25 m/s的速度沿水平方向反弹，落地点到墙面的距离在10 m至15 m之间，忽略空气阻力，取g＝10 m/s²，球在墙面上反弹点的高度范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．0.8 m至1.8　 m 　　　　　　　　B．0.8 m至1.6 m

C．1.0 m至1.6 m　　　　　　　　 　D．1.0 m至1.8 m

解析：球落地时所用时间在t₁＝＝0.4 s至t₂＝＝0.6 s之间，所以反弹点的高度在h₁＝gt₁²＝0.8 m至h₂＝ gt₂²＝1.8 m之间，故选A.

答案：A

3．(2008·全国卷Ⅰ)如图2所示，一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上．物体与斜面接触时速度与水平方向的夹角φ满足　　　　　　　 　　(　)

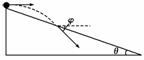
图2

A．tanφ＝sinθ　　　　　　　　 　B．tanφ＝cosθ

C．tanφ＝tanθ 　　　　　　　　D．tanφ＝2tanθ

解析：竖直速度与水平速度之比为：tanφ＝，竖直位移与水平位移之比为：tanθ＝，故tanφ＝2tanθ，D正确．

答案：D

2. (2010·江南十校模拟)如图1所示，某同学为了找出平抛运动物体的初速　

度之间的关系，用一个小球在O点对准前方的一块竖直放置的挡板，O

与A在同一高度，小球的水平初速度分别是v₁、v₂、v₃，打在挡板上的

位置分别是B、C、D，且AB∶BC∶CD＝1∶3∶5.则v₁、v₂、v₃之间的

正确关系是　　　　　　　　　　　　　　　　　　　　　　　 (　) 　　　　　图1

A．v₁∶v₂∶v₃＝3∶2∶1

B．v₁∶v₂∶v₃＝5∶3∶1

C．v₁∶v₂∶v₃＝6∶3∶2

D．v₁∶v₂∶v₃＝9∶4∶1

解析：在竖直方向上，由t＝ 得小球落到B、C、D所需的时间比t₁∶t₂∶t₃＝∶∶＝∶∶＝1∶2∶3；在水平方向上，由v＝得：v₁∶v₂∶v₃＝∶∶＝6∶3∶2.

答案：C

1．(2008·广东高考)从水平飞行的直升机上向外自由释放一个物体，不计空气阻力，在物体下落过程中，下列说法正确的是　　　　　　　　　　　　　　　　　　　　 (　)

A．从飞机上看，物体静止

B．从飞机上看，物体始终在飞机的后方

C．从地面上看，物体做平抛运动

D．从地面上看，物体做自由落体运动

解析：在匀速飞行的飞机上释放物体，物体有一水平速度，故从地面上看，物体做平抛运动，C对D错；飞机的速度与物体水平方向上的速度相同，故物体始终在飞机的正下方，且相对飞机的竖直位移越来越大，A、B错．

答案：C

12．(14分)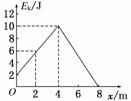质量m＝1 kg的物体，在水平拉力F(拉力方向与物体初速度方向相同)　

的作用下，沿粗糙水平面运动，经过位移4 m时，拉力F停止作用，运动到位

移是8 m时物体停止，运动过程中E_k－x的图线如图10所示．求：(g取10 m/s²)

(1)物体的初速度多大？

(2)物体和平面间的动摩擦因数为多大？　　　　 　　　　　　　　　　　　　　图10

(3)拉力F的大小．

解析：(1)从图线可知初动能为2 J，

E_k0＝mv²＝2 J，v＝2 m/s.

(2)在位移4 m处物体的动能为10 J，在位移8 m处物体的动能为零，这段过程中物体克

服摩擦力做功．

设摩擦力为F_f，则

－F_fx₂＝0－10 J＝－10 J

F_f＝ N＝2.5 N

因F_f＝μmg

故μ＝＝＝0.25.

(3)物体从开始到移动4 m这段过程中，受拉力F和摩擦力F_f的作用，合力为F－F_f，

根据动能定理有

(F－F_f)·x₁＝ΔE_k

故得F＝+F_f＝(+2.5) N＝4.5 N.

答案：(1)2 m/s　(2)0.25　(3)4.5 N

11．(12分)右端连有光滑弧形槽的水平桌面AB长L＝1.5 m，如图9所示．将一个质量为m＝0.5 kg的木块在F＝1.5 N的水平拉力作用下，从桌面上的A端由静止开始向右运动，木块到达B端时撤去拉力F，木块与水平桌面间的动摩擦因数μ＝0.2，取g＝10 m/s².求：　　　　　　　　 图9

(1)木块沿弧形槽上升的最大高度；

(2)木块沿弧形槽滑回B端后，在水平桌面上滑动的最大距离．

解析：(1)由动能定理得：

FL－F_fL－mgh＝0

其中F_f＝μF_N＝μmg＝0.2×0.5×10 N＝1.0 N

所以h＝＝ m＝0.15 m

(2)由动能定理得：

mgh－F_fx＝0

所以x＝＝ m＝0.75 m

答案：(1)0.15 m　(2)0.75 m

10.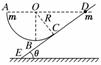 (11分)如图8所示，竖直固定放置的斜面DE与一光滑的圆弧轨道ABC相连，C为切点，

圆弧轨道的半径为R，斜面的倾角为θ.现有一质量为m的滑块从D点无初速下滑，滑块可在斜面和圆弧轨道之间做往复运动，已知圆弧轨道的圆心O与A、D在同一水平面上，滑块与斜面间的动摩擦因数为μ，求：

(1)滑块第一次至左侧AC弧上时距A点的最小高度差h.

(2)滑块在斜面上能通过的最大路程s.

解析：(1)由动能定理得：

mgh－μmgcosθ·R/tanθ＝0

得h＝μRcos²θ/sinθ＝μRcosθcotθ

(2)滑块最终至C点的速度为0时对应在斜面上的总路程最大，由动能定理得

mgRcosθ－μmgcosθ·s＝0

得：s＝.

答案：(1)μRcosθcotθ　(2)

9.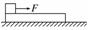如图7所示，质量为M、长度为L的木板静止在光滑的水平面上，质量为m的小物体(可视为质点)放在木板上最左端，现用一水平恒力F作用在小物体上，使物体从静止开始做匀加速直线运动．已知物体和木板之间的摩擦力为F_f.当物体滑到木板的最右端时，木板运动的距离为x，则在此过程中　 (　)

A．物体到达木板最右端时具有的动能为(F－F_f)(L+x)

B．物体到达木板最右端时，木板具有的动能为F_fx

C．物体克服摩擦力所做的功为F_fL

D．物体和木板增加的机械能为Fx

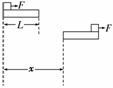
解析：由题意画示意图可知，由动能定理对小物体：(F-F_f)·(L+x)= mv²，故A正确．对木板：F_f·x=Mv²，故B正确．物块克服摩擦力所做的功F_f·(L+x)，故C错．物块和木板增加的机械能

mv²+Mv²=F·(L+x)-F_f·L=(F-F_f)·L+F·x，故D错．

答案：AB