
1 求证:
求证:
证明:左边= =右边
=右边
或:右边=tan(x- )
)
= =左边
=左边
2 若0<α<β<
若0<α<β< ,sinα+cosα=
,sinα+cosα=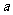 ,sinβ+cosβ=b,则
,sinβ+cosβ=b,则
A ab<1
B
ab<1
B a>b
a>b
C a<b
D
a<b
D ab>2
ab>2
解:sinα+cosα=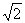 sin(α+
sin(α+ )=a
)=a
sinβ+cosβ=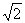 sin(β+
sin(β+ )=b
)=b
又∵0<α<β<
∴0<α+ <β+
<β+ <
<
∴sin(α+ )<sin(β+
)<sin(β+ )
)
∴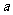 <b
<b
答案:C
1 在△ABC中,ÐC>90°,则tanAtanB与1的关系适合………………(B)
在△ABC中,ÐC>90°,则tanAtanB与1的关系适合………………(B)
(A) tanAtanB>1 (B) tanAtanB>1 (C) tanAtanB =1 (D)不确定
解:在△ABC中 ∵ÐC>90° ∴A, B为锐角 即tanA>0, tanB>0
又tanC<0 于是:tanC
= -tan(A+B) =  <0
<0
∴1 - tanAtanB>0 即:tanAtanB<1
又解:在△ABC中 ∵ÐC>90° ∴C必在以AB为直径的⊙O内(如图)

|
设CD = h,C’D = h’,AD = p,BD = q,
|
|
|

2.设a,bÎ( ,
, ),tana、tanb是一元二次方程
),tana、tanb是一元二次方程 的两个根,求 a + b
的两个根,求 a + b
解:由韦达定理: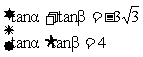
∴
又由a,bÎ( ,
, )且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
)且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
得a + bÎ (-p, 0) ∴a + b = 
例1 若tana=3x,tanb=3-x, 且a-b=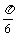 ,求x的值
,求x的值
解:tan(a-b)=tan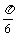 =
= ∵tana=3x,tanb=3-x
∵tana=3x,tanb=3-x
∴
∴3•3x-3•3-x=2 即:
即:
∴ (舍去)
∴
(舍去)
∴
例2 已知锐角a, b, g 满足sina+sing=sinb, cosa-cosg=cosb, 求a-b的值
解: ∵sina+sing=sinb ∴sina -sinb = -sing <0 ①
∴sina <sinb ∴a<b
同理:∵cosa-cosg=cosb ∴ cosa- cosb = cosg ②
①2+②2: 1+1-2cos(a-b)=1 ∴cos(a-b)=
∵
 ∴
∴ ∴a-b=
∴a-b=
例3 已知tana,tanb是关于x的方程 的两个实根,求tan(a+b)的取值范围
的两个实根,求tan(a+b)的取值范围
解:∵tana,tanb是方程 的两个实根
的两个实根
∴△=4(7m-3)-8m2≥0 ∴2m2-7m+3≤0 解之: ≤m≤3
≤m≤3
又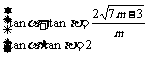 ∴
∴
为求范围: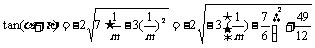
∵ ≤m≤3 ∴
≤m≤3 ∴ ≤m≤2
≤m≤2
∴当 时,
时, 有最大值
有最大值
当 或
或 时,
时, 有最小值2
有最小值2
∴
即 
∴p-q+1=0
例4 若 ,求f (x)=
,求f (x)= sinx+cosx的最大值和最小值,并求出此时的x值
sinx+cosx的最大值和最小值,并求出此时的x值
解:
f (x)= sinx+cosx=2
sinx+cosx=2
∵ ∴
∴
∴

即
当且仅当 ,
, 时 f (x)min=
时 f (x)min=
当且仅当 ,
, 时 f (x)max=2
时 f (x)max=2
例5 已知f (x)=-acos2x- asin2x+2a+b,其中a>0,xÎ[0,
asin2x+2a+b,其中a>0,xÎ[0,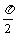 ]时,
]时,
-5≤f (x)≤1,设g(t)=at2+bt-3,tÎ[-1,0],求g(t)的最小值
解: f (x)=-acos2x- asin2x+2a+b=-2a[
asin2x+2a+b=-2a[ sin2x+
sin2x+ cos2x]+2a+b
cos2x]+2a+b
=-2asin(2x+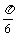 )+2a+b
)+2a+b
∵xÎ[0,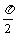 ] ∴
] ∴
∴
又 a>0 ∴-2a<0 ∴
∴
∴
∵-5≤f (x)≤1
∴
∴g(t)=at2+bt-3=2t2-5t-3=2(t- )2-
)2-
∵tÎ[-1,0]
∴当t=0时,g(t)min=g(0)=-3
1.两角和与差的正、余弦公式



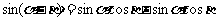


20、(本题满分16分)
已知数列 ,设
,设
 ,数列
,数列 。
。
(1)求证: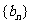 是等差数列;
是等差数列;
(2)求数列 的前n项和Sn;
的前n项和Sn;
(3)若 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围.
19.(本题满分16分)已知函数f(x)=alnx―ax―3(a∈R).
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意t∈[1,2],
函数g(x)=x3+x2[f′(x)+]在区间(t,3)上总不是单调函数,求m的取值范围.
18. (本题满分14分)
某地产开发公司拟在如图所示夹角为60°的角形区域BAC内进行地产开发。根据市政府要求,此地产开发必须在角形区域的两边建一条定长为500m的绿化带PQ,并且规定由此绿化带和角形区域围成的△APQ的面积作为此开发商的开发面积。问开发商如何给P,Q进行选址,才能使自己的开发面积最大?并求最大开发面积。

17.(本题满分15分)△ 中,
中, 所对的边分别为
所对的边分别为 ,
, ,
, .
.
(1)求 ; (2)若
; (2)若 ,求
,求 。
。
16.(本小题满分14分)
已知:命题 集合
集合 ,
, ,且
,且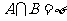
(I)若命题q为真命题,求实数 的取值范围;
的取值范围;
(II)若命题
 ,且
,且 ,试求实数
,试求实数 的取值范围,使得命题
的取值范围,使得命题 有且只有一个为真命题.
有且只有一个为真命题.
15.(本题满分14分)
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
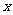
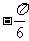














(Ⅰ)根据表格提供的数据求函数 的一个解析式;
的一个解析式;
(Ⅱ)根据(1)的结果,若函数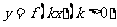 周期为
周期为 ,当
,当 时,方程
时,方程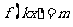 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围;
的取值范围;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com