
4°角变换 5°“升幂”与“降次” 6°辅助角
1 已知 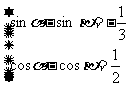

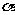 、
、 均为锐角,求
均为锐角,求 的值.
的值.
分析:由于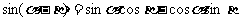 ,由已知两式一时得不到
,由已知两式一时得不到 与
与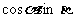 的值,而只能出现
的值,而只能出现 与
与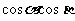 一类的值,例如
一类的值,例如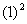 +
+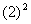 ,得
,得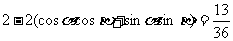 ,化简、整理得
,化简、整理得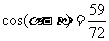 .由此要求
.由此要求 的值,固然有路可循,但是还要进一步定出
的值,固然有路可循,但是还要进一步定出 的值的符号才行.
的值的符号才行.
2 已知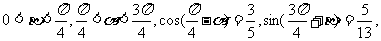 求
求 的值.
的值.
提示: =
=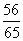 .
.
3 已知 求证
求证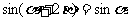 .
.
分析:比较已知与求证部分,必然要做如下变换为宜: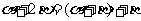 .
.
解: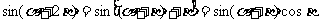 ,
,
而 ,注意到
,注意到 ,得
,得
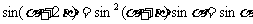
例1(辅助角)函数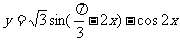 的最小值
的最小值
解: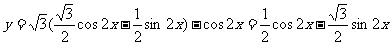
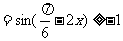
例2(角变换)已知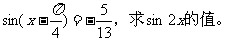
解: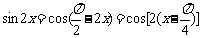
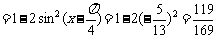
例3(公式逆用)计算:(1 + )tan15°-
)tan15°-
解:原式= (tan45°+ tan60°)tan15°-
=tan105°(1-tan45°tan60°)tan15° -
= (1 - ) tan105° tan15° -
) tan105° tan15° - = (1 -
= (1 - )×(- 1)-
)×(- 1)- = - 1
= - 1
例4(角变换)已知sin(45° - a) = 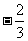 ,且45° < a < 90°,求sina
,且45° < a < 90°,求sina
解:∵45° <
a < 90° ∴-45° < 45°-a < 0° ∴cos(45°-a) = 
cos2a = sin(90°-2a) = sin[2(45°-a)]
= 2sin(45°-a)cos(45°-a) =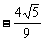
即 1 - sin2a = 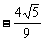 , 解之得:sina =
, 解之得:sina = 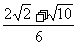
例5已知q是三角形中的一个最小的内角,
且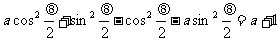 ,求a的取值范围
,求a的取值范围
解:原式变形: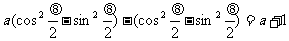
即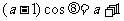 ,显然
,显然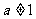 (若
(若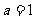 ,则 0 = 2)
,则 0 = 2)
∴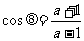
又∵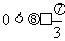 ,∴
,∴
即 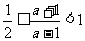 解之得:
解之得:
例6试求函数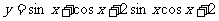 的最大值和最小值
的最大值和最小值 若
若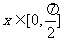 呢?
呢?
解:1.设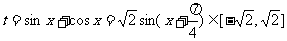
则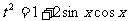 ∴
∴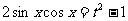
∴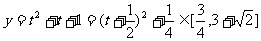
∴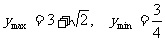
2.若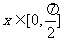 ,则
,则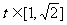 ,∴
,∴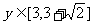
即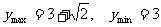
例7 已知tana = 3tan(a + b),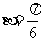 ,求sin(2a + b)的值
,求sin(2a + b)的值
解:由题设: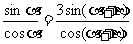 即sina cos(a + b) = 3sin(a + b)cosa
即sina cos(a + b) = 3sin(a + b)cosa
即sin(a + b) cosa + cos(a + b)sina = 2sina cos(a + b) - 2cosasin(a + b)
∴sin(2a + b) = -2sinb 又∵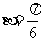 ∴sinb
∴sinb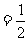 ∴sin(2a + b) = -1
∴sin(2a + b) = -1
1.两角和与差的正、余弦公式
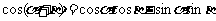
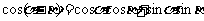

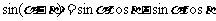
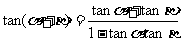
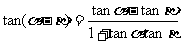
2 推导公式:
推导公式:
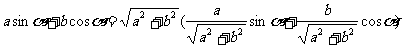
由于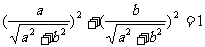
sin2θ+cos2θ=1
(1)若令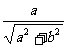 =sinθ,则
=sinθ,则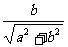 =cosθ
=cosθ
∴asinα+bcosα=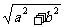 (sinθsinα+cosθcosα)=
(sinθsinα+cosθcosα)=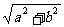 cos(θ-α)
cos(θ-α)
或= cos(α-θ)
cos(α-θ)
(2)若令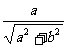 =cos
=cos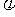 ,则
,则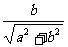 =sin
=sin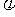
∴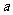 sinα+bcosα=
sinα+bcosα= (sinαcos
(sinαcos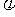 +cosαsin
+cosαsin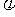 )=
)= sin(α+
sin(α+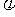 )
)
例如:2sinθ+cosθ=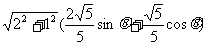
若令cos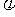 =
=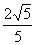 ,则sin
,则sin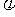 =
=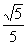
∴2sinθ+cosθ= (sinθcos
(sinθcos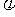 +cosθsin
+cosθsin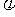 )=
)= sin(θ+
sin(θ+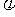 )
)
若令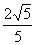 =sinβ,则
=sinβ,则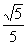 =cosβ
=cosβ
∴2sinθ+cosθ= (cosθcosβ+sinθsinβ)=
(cosθcosβ+sinθsinβ)= cos(θ-β)或
cos(θ-β)或
= cos(β-θ)
cos(β-θ)
看来,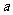 sinθ+bcosθ均可化为某一个角的三角函数形式,且有两种形式
sinθ+bcosθ均可化为某一个角的三角函数形式,且有两种形式
22.(本小题满分14分)已知函数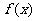 是一次函数,且
是一次函数,且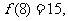
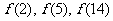 成等比数列,设
成等比数列,设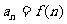 ,(
,( 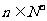 )
)
(1)求数列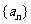 的前n项和Tn;
的前n项和Tn;
(2)设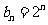 ,求数列
,求数列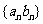 的前n项和
的前n项和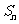 。
。
21.(本小题满分12分)
在等比数列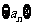 中,
中,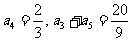 .
.
(I)求数列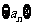 的通项公式;
的通项公式;
(II)若数列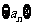 的公比大于
的公比大于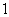 ,且
,且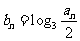 ,求数列
,求数列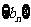 的前
的前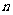 项和
项和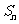 .
.
20.(本小题满分12分)
已知数列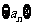 的前n项和公式为
的前n项和公式为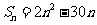 。
。
(1)这个数列是等差数列吗?求出它的通项公式;
(2)求使得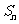 最小的序号n的值。
最小的序号n的值。
19.(本小题满分12分)
(理科)某工厂前年1月份的产值为a元,月平均增长率为P(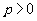 )。
)。
(1)求这个工厂前年全年产值的总和;
(2)如果该工厂的月平均增长率一直为p,试求该工厂产值的年平均增长率。
(文科)已知等差数列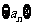 中,
中,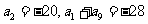 .
.
⑴求数列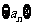 的通项公式;
的通项公式;
⑵若数列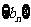 满足
满足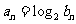 ,设
,设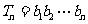 ,且
,且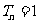 ,求
,求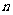 的值.
的值.
17、(本小题满分12分)已知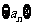 是等差数列,其中
是等差数列,其中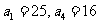
(1)求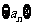 的通项; (2)数列
的通项; (2)数列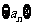 从哪一项开始小于0;
从哪一项开始小于0;
(3)求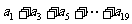 值。
值。
18(本小题满分12分)
等差数列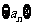 中,
中,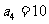 且
且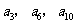 成等比数列,求数列
成等比数列,求数列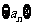 前20项的和
前20项的和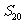 .
.
13.已知等比数列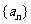 的公比
的公比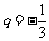 ,则
,则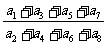 等于 。
等于 。
14 等差数列{an},{bn}的前n项和分别为Sn,Tn,若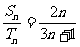 ,则
,则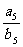 =_
_
=_
_
15已知数列{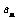 }通项公式为
}通项公式为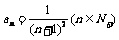 ,记
,记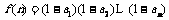 ,试通过求
,试通过求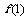 ,
, ,
,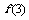 的值,推测出
的值,推测出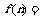
16等差数列{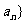 中,
中,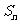 是它的前n项的和,且
是它的前n项的和,且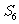 <
<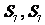 >
>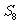 给出下列命题
给出下列命题
① 数列中前7项是递增的,从第8开始递减; ②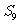 一定小于
一定小于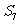 ;③
;③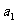 是各项中最大的;④
是各项中最大的;④ 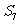 不一定是
不一定是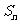 的最大值; 其中正确的命题的序号是 。
的最大值; 其中正确的命题的序号是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com