
|
|
内容 |
要求 |
||
|
A |
B |
C |
||
|
1 |
棱柱、棱锥、球的概念 |
√ |
|
|
|
2 |
棱柱、正棱锥、球的性质 |
|
√ |
|
|
3 |
球的表面积, 柱、锥、球的体积公式. |
|
√ |
|
22.解:①由ax +(b-1)x+c=0无实根,得Δ
+(b-1)x+c=0无实根,得Δ =(b-1)
=(b-1)  -4ac<0
-4ac<0
由ax +(b+1)x+c=0无实根,得Δ
+(b+1)x+c=0无实根,得Δ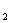 =(b+1)
=(b+1)  -4ac<0,
-4ac<0,
两式相加得:4ac-b >1,
>1,
②∵4ac-b >1>0,∴a(x+
>1>0,∴a(x+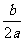 )
) 与
与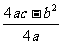 同号,
同号,
∴|ax+bx+c|=|a(x+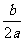 )
) +
+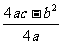 |=|a|(x+
|=|a|(x+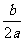 )
) +
+ ≥
≥ >
>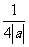
21.解:(1)解: ,
, ,
, 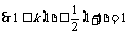 ,
, 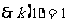
(2)解:

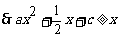 ,
, 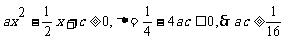 ,
,
又 即
即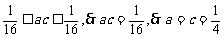
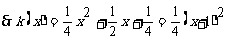
(3)证明: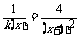
∴原式 …
…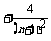
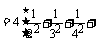 …
…
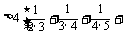 …
…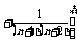
 …
…
20、解:(1)∵方程f (x)-x=0的两根为x1、x2,
∴(x2-x1)2=(x2+x1)2-4x1x2=b2-2b+1-4c.
∵x2-x1>1,∴b2-2b+1-4c>1.
∴b2>2(b+2c).
(2)∵x1是方程f (x)-x=0的根,∴x1=f (x1).
∴f (t)-x1=f (t)-f (x1)=(t-x1)(t+x1+b)=(t-x1)(t+1-x2).
∵0<t<x1,∴t-x1<0.
∵x2-x1>1,∴x1+1-x2<0.
∴t+1-x2<x1+1-x2<0.故f (t)-x1>0.
(3)∵x∈[-1,1]时,恒有|f (x)|≤1,
∴|f (0)|=|c|≤1,|f (1)|=|1+b+c|≤1.
∴|1+b|=|1+b+c-c|≤|1+b+c|+|-c|=|1+b+c|+|c|≤1+1=2.
19、解:(文)(1)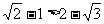 ,
, 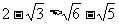
(2)一般结论:若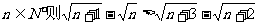 成立
成立
证明 欲证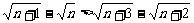 成立
成立
只需证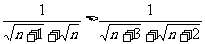
也就是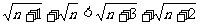 (
( )
)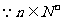
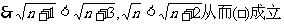
故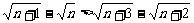
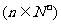
(理)解先考查两个变量的情形
(1-a)(1-b)=1-a-b+ab≥1-a-b 当且仅当a、b中至少有1个为零时,等号成立
∴(1-a)(1-b)(1-c) ≥(1-a-b)(1-c)=1-a-b-c+c(a+b) ≥1-a-b-c 当且仅当a、b、c中至少有2个为零时,等号成立
于是(1-a)(1-b)(1-c)(1-d)≥1-a-b-c-d, 当且仅当a、b 、c、d 中至少有3个为零时,等号成立 ∴a、b、c、d至少有3个为0时,M=N,否则M>N .
18.证: 要证明原不等式成立,则只要证: 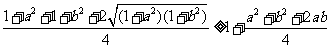
只要证: 
若 ,上式显然成立,从而原不等式成立;
,上式显然成立,从而原不等式成立;
若1+ab>0,则只要证: 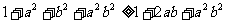
只要证: 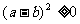
上式显然成立,从而原不等式成立。
17、解:(1)因为
所以
由条件 ,消去
,消去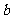 得
得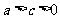
由条件 ,消去
,消去 得
得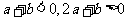
故
(2)由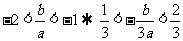
又因为
而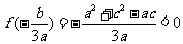
所以方程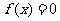 在区间
在区间 与
与 内分别有一实根。
内分别有一实根。
13、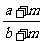
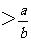 14、
14、 ③
15、
③
15、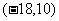 16、B
16、B
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
B |
12 |
|
B |
C |
B |
A |
C |
D |
C |
A |
A |
C |
B |
D |
22.设二次函数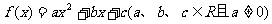 ,若函数
,若函数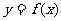 的图象与直线
的图象与直线 和
和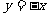 均无公共点。
均无公共点。
(1)求证:
(2)求证:对于一切实数 恒有
恒有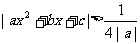
高三第一轮复习训练题
数学(十)(不等式1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com