
10.从数字0、1、3、5、7中取出不同的三个作系数,可组成多少个不同的一元二次方程ax2+bx+c=0?其中有实数根的有几个?
分析:(1)二次方程要求a不为0,故a只能在1、3、5、7中选,b、c没有限制.
(2)二次方程要有实根,需Δ=b2-4ac≥0,再对c分类讨论.
解:(1)a只能在1、3、5、7中选一个有A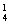 种,b、c可在余下的4个中任取2个,有A
种,b、c可在余下的4个中任取2个,有A 种.故可组成二次方程A
种.故可组成二次方程A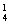 ·A
·A =48个.
=48个.
(2)方程要有实根,需Δ=b2-4ac≥0.
c=0,a、b可在1、3、5、7中任取2个,有A 种;
种;
c≠0,b只能取5、7,b取5时,a、c只能取1、3,共有A 个;b取7时,a、c可取1、3或1、5,有2A
个;b取7时,a、c可取1、3或1、5,有2A 个.故有实根的二次方程共有A
个.故有实根的二次方程共有A +A
+A +2A
+2A =18个.
=18个.
9.关于正整数2160,求:
(1)它有多少个不同的正因数?
(2)它的所有正因数的和是多少?
解:(1)∵N=2160=24×33×5,
∴2160的正因数为P=2α×3β×5γ,
其中α=0,1,2,3,4,β=0,1,2,3,γ=0,1.
∴2160的正因数共有5×4×2=40个.
(2)式子(20+21+22+23+24)×(30+31+32+33)×(50+51)的展开式就是40个正因数.
∴正因数之和为31×40×6=7440.
8.一只青蛙从正六边形ABCDEF的顶点A处起跳,每次可以跳到与它相邻的两个顶点之一,若5步内(含5步)跳到顶点D则停止,5步跳不到D点也停止,问共有多少种不同的跳法?
解法1:3步跳到D点的有2种方法。
5步跳到或跳不到D点的共有 25-2×22=24种方法,(其中2×22是3步跳到D后还继续跳的)。所以,共有不同跳法 2+24=26 (种)

 解法2:画树图
解法2:画树图
共有(1+22+23)×2=26(种)。
7.(2003年全国)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色.现有4种颜色可供选择,则不同的着色方法共有_____________种.(以数字作答)

练习简答:1-3.BCC; 4..448; 5. 2400;.
6分首位是2、3、4分别计算:(1+C ·A
·A +C
+C ·A
·A )+ A
)+ A +C
+C ·A
·A =58; 7.依次染①、②、③、④、⑤.故有4×3×2×(1+2)=72种.
=58; 7.依次染①、②、③、④、⑤.故有4×3×2×(1+2)=72种.
[解答题]
6.(2004四川模拟)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有__________.
5.(2006全国Ⅰ)安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种 (用数字作答)
(用数字作答)
4.在所有无重复数字的四位数中,千位上的数字比个位上的数字大2的数共有____个.
3. 6个人并排站成一排,B站在A的右边,C站在B的右边,则不同的排法总数为
A.  B.
B.  C.
C.  D.
D.  ( )
( )
[填空题]
2.若2n个学生排成一排的排法数为x,这2n个学生排成前后两排,每排各n个学生的排法数为y,则x、y的关系为 ( )
A.x>y B.x<y C.x=y D.x=2y
1.从长度分别为1、2、3、4的四条线段中,任取三条的不同取法共有n种,在这些取法中,以取出的三条线段为边可组成的三角形的个数为m,则 等于 ( )
等于 ( )
A.0 B. C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com