
4、椭圆、双曲线的通径(最短弦)为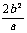 ,焦准距为p=
,焦准距为p=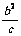 ,抛物线的通径为2p,焦准距为p; 双曲线
,抛物线的通径为2p,焦准距为p; 双曲线 (a>0,b>0)的焦点到渐近线的距离为b;
(a>0,b>0)的焦点到渐近线的距离为b;
3. 已知弦AB的中点,研究AB的斜率和方程。
(1)AB是椭圆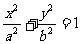 (
(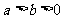 )的一条弦,中点M坐标为
)的一条弦,中点M坐标为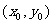 ,则AB的斜率为
,则AB的斜率为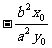 ,运用点差法求AB的斜率,设
,运用点差法求AB的斜率,设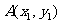 ,
,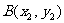 。A、B都在椭圆上,
。A、B都在椭圆上,
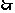
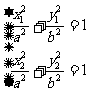 ,
,
两式相减得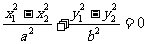 。
。
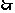
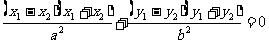 ,
,
即 。故
。故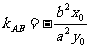 。
。
(2)运用类比的手法可以推出,已知AB是双曲线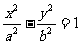 的弦,中点
的弦,中点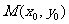 ,则
,则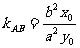 ;
;
(3)已知抛物线 (
(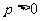 )的弦AB的中点
)的弦AB的中点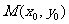 ,则
,则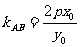 。
。
2. 连结圆锥曲线上的两点的线段称为圆锥曲线的弦。
直线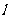 :
: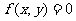 ,曲线
,曲线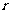 :
: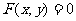 ,
,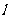 与
与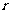 的两个不同的交点A、B,
的两个不同的交点A、B,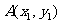 ,
,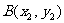 ,则
,则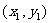 ,
,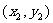 是方程组
是方程组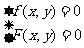 的两组解,方程组消元后化为关于
的两组解,方程组消元后化为关于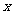 (或者
(或者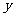 )的一元二次方程
)的一元二次方程 (
(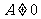 ),判别式
),判别式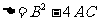 ,应有
,应有 ,所以
,所以 、
、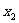 是方程
是方程 的解,由根与系数的关系(韦达定理)求出
的解,由根与系数的关系(韦达定理)求出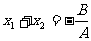 ,
,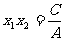 。所以A、B两点间距离为
。所以A、B两点间距离为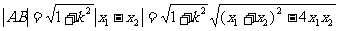 ,即弦长公式。也可以写成关于
,即弦长公式。也可以写成关于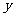 的形式,其弦长公式为
的形式,其弦长公式为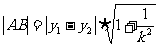 。
。
1. 判断直线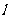 与圆锥曲线
与圆锥曲线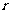 的位置关系时,通常将直线
的位置关系时,通常将直线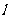 的方程
的方程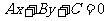 (A、B不同时为0)代入圆锥曲线
(A、B不同时为0)代入圆锥曲线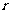 的方程
的方程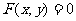 。消去
。消去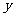 (也可以消去
(也可以消去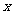 )得到一个关于变量
)得到一个关于变量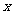 (或者变量
(或者变量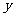 )的一元二次方程。
)的一元二次方程。
即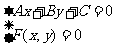 ,消去
,消去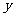 后的
后的 。
。
(1)当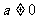 时,则有
时,则有 ,直线
,直线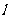 与曲线
与曲线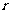 相交;
相交; ,直线
,直线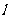 与曲线
与曲线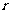 相切;
相切; ,直线
,直线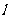 与曲线
与曲线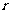 相离。
相离。
(2)当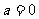 时,即得到一个一次方程,则
时,即得到一个一次方程,则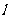 与
与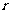 相交,且只有一个交点,此时,若
相交,且只有一个交点,此时,若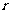 为双曲线,则直线
为双曲线,则直线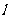 与双曲线的渐近线是平行;若
与双曲线的渐近线是平行;若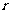 为抛物线,则直线
为抛物线,则直线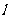 与抛物线的对称轴的位置关系是平行。
与抛物线的对称轴的位置关系是平行。
掌握直线与圆锥曲线的位置关系的判断方法,能够正确熟练地解决与直线和圆锥曲线的位置关系相关的一些问题。这类问题常涉及到圆锥曲线的性质和直线的基本知识点、线段的中点、弦长、垂直问题,因此分析问题时利用数形结合思想和设而不求法与弦长公式及韦达定理联系去解决。
圆锥曲线与直线的位置关系
10、想像:在原有的感性形象的基础上,创造新形象的心理过程。
作用:为塑造形象、表现主题服务。使读者接受美的陶冶。
9、联想:由一事物想到另一事物的心理过程。
作用:丰富文章内容,使人物形象更丰满,性格更鲜明突出,情节更生动感人。
8、照应
作用:记叙文:使文章浑然一体,整体感强,突出主题。议论文:强化××论点。 散文:反复地抒发××情感,增加情感的深度。
7、伏笔和铺垫
作用:内容前后照应,情节严丝合缝。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com