
1(嘉定区2008-2009第一次质量调研第19题)(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
 如图,一船在海上由西向东航行,在
如图,一船在海上由西向东航行,在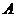 处测得某岛
处测得某岛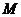 的方位角为北偏东
的方位角为北偏东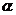 角,前进
角,前进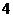
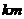 后在
后在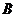 处测得该岛的方位角为北偏东
处测得该岛的方位角为北偏东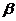 角,已知该岛周围
角,已知该岛周围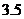
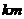 范围内有暗礁,现该船继续东行.
范围内有暗礁,现该船继续东行.
(1)若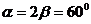 ,问该船有无触礁危险?
,问该船有无触礁危险?
如果没有,请说明理由;如果有,那么该船自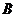 处向
处向
东航行多少距离会有触礁危险?
(2)当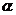 与
与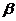 满足什么条件时,该船没有触礁危险?
满足什么条件时,该船没有触礁危险?
答案:解:(1)作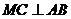 ,垂足为
,垂足为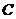 ,
,
由已知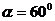 ,
,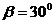 ,所以
,所以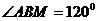 ,
,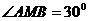
 所以
所以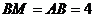 ,
,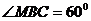 ,……(2分)
,……(2分)
所以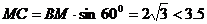 ,
,
所以该船有触礁的危险.……(4分)
设该船自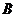 向东航行至点
向东航行至点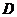 有触礁危险,
有触礁危险,
则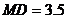 ,……(5分)
,……(5分)
在△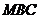 中,
中,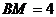 ,
,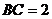 ,
,
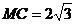 ,
,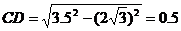 ,
,
所以,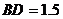 (
(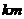 ).……(7分)
).……(7分)
所以,该船自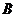 向东航行
向东航行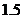
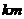 会有触礁危险.……(8分)
会有触礁危险.……(8分)
(2)设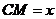 ,在△
,在△ 中,由正弦定理得,
中,由正弦定理得,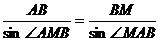 ,
,
即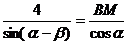 ,
,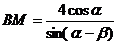 ,……(10分)
,……(10分)
而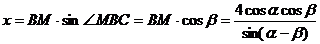 ,……(12分)
,……(12分)
所以,当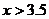 ,即
,即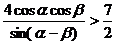 ,
,
即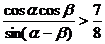 时,该船没有触礁危险.……(14分)
时,该船没有触礁危险.……(14分)
2(2008学年度第一学期上海市普陀区高三年级质量调研第19题)(本题满分16分,第1小题10分,第2小题6分)
在某个旅游业为主的地区,每年各个月份从事旅游服务工作的人数会发生周期性的变化. 现假设该地区每年各个月份从事旅游服务工作的人数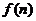 可近似地用函数
可近似地用函数 来刻画. 其中:正整数
来刻画. 其中:正整数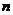 表示月份且
表示月份且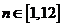 ,例如
,例如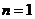 时表示1月份;
时表示1月份;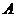 和
和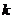 是正整数;
是正整数;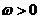 .
.
统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
① 各年相同的月份,该地区从事旅游服务工作的人数基本相同;
② 该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人;
③ 2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.
(1)
试根据已知信息,确定一个符合条件的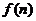 的表达式;
的表达式;
(2) 一般地,当该地区从事旅游服务工作的人数超过400人时,该地区也进入了一年中的旅游“旺季”. 那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.
答案:
|
解:(1)根据三条规律,可知该函数为周期函数,且周期为12. 由此可得, 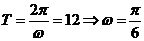 ; ;由规律②可知, 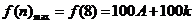 , ,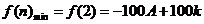 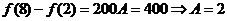 ; ;又当 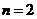 时, 时,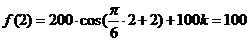 , ,所以, 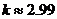 ,由条件 ,由条件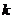 是正整数,故取 是正整数,故取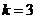 . .综上可得, 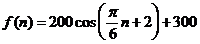 符合条件. 符合条件.(2) 解法一:由条件, 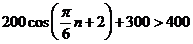 ,可得 ,可得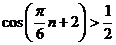 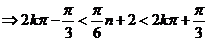 , ,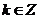 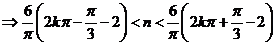 , ,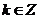 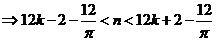 , ,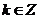 . .因为 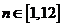 , ,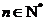 ,所以当 ,所以当 时, 时,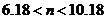 , ,故 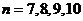 ,即一年中的7,8,9,10四个月是该地区的旅游“旺季”. ,即一年中的7,8,9,10四个月是该地区的旅游“旺季”.解法二:列表,用计算器可算得
故一年中的7,8,9,10四个月是该地区的旅游“旺季”. |
…3 …6 …9 …10 …12 …14 …16 …15 …16 |
3 (闸北区09届高三数学(理)第14题)(本小题满分14分)
在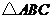 中,内角
中,内角 所对的边长分别是
所对的边长分别是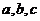 .
.
(Ⅰ)若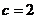 ,
,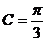 ,且
,且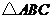 的面积
的面积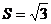 ,求
,求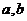 的值;
的值;
(Ⅱ)若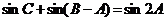 ,试判断
,试判断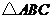 的形状.
的形状.
答案:解:(Ⅰ)由余弦定理及已知条件得,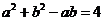 ,………………………………….3分
,………………………………….3分
又因为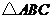 的面积等于
的面积等于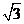 ,所以
,所以 ,得
,得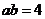 .···························· 2分
.···························· 2分
联立方程组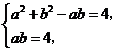 解得
解得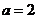 ,
,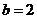 .······················································ 2分
.······················································ 2分
(Ⅱ)由题意得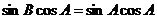 ,·································································· 3分
,·································································· 3分
当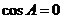 时,
时,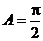 ,
,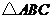 为直角三角形··························································· 2分
为直角三角形··························································· 2分
当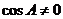 时,得
时,得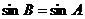 ,由正弦定理得
,由正弦定理得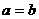 ,
,
所以,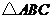 为等腰三角形.····················································································· 2分
为等腰三角形.····················································································· 2分
4 (上海市静安区2008学年高三年级第一次质量调研第17题)(本题满分12分)第1小题满分5分,第2小题满分7分.
(理)设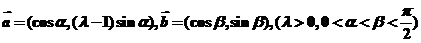 是平面上的两个向量,若向量
是平面上的两个向量,若向量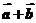 与
与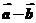 相互垂直,
相互垂直,
(1)求实数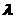 的值;
的值;
(2)若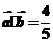 ,且
,且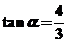 ,求
,求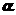 的值(结果用反三角函数值表示)
的值(结果用反三角函数值表示)
答案:解:(1)由题设,得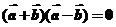 ,即
,即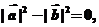
所以,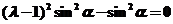 ,即
,即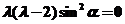
因为 ,
,
所以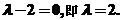
(2)由(1)知,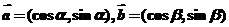 ,
,
 ,又
,又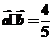 ,
,
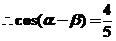 ,
,
(解法1)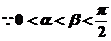 ,
,
则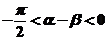 ,
,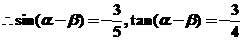
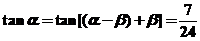 ,又
,又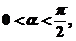

(解法2)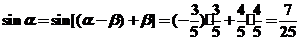 ,又
,又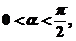
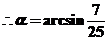
5 (文)已知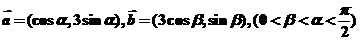 是平面上的两个向量.
是平面上的两个向量.
(1)试用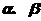 表示
表示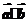 ;
;
(2)若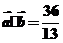 ,且
,且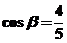 ,求
,求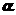 的值(结果用反三角函数值表示)
的值(结果用反三角函数值表示)
答案:解:(1) 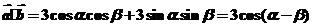 ;
;
(2)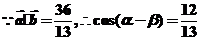 ,
,
又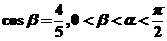 ,
,
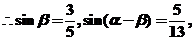
(解法1) 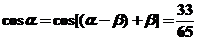 ,
,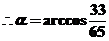
(解法2)  ,
,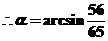
6已知角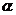 的顶点在原点,始边与
的顶点在原点,始边与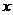 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点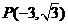 .
.
(1)解关于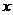 的方程:
的方程: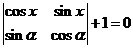 ;
;
(2)若函数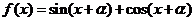 (
(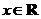 )的图像关于直线
)的图像关于直线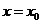 对称,求
对称,求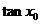 的值.
的值.
答案:(1)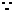 角
角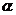 终边经过点
终边经过点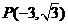 ,∴
,∴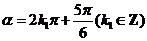 . (2分)
. (2分)
∴由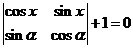 可得:
可得: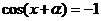 (4分)
(4分)
 , ∴
, ∴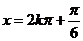
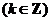 . (6分)
. (6分)
(2)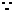
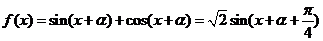 (
(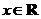 ) (2分)
) (2分)
且函数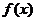 的图像关于直线
的图像关于直线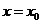 对称,
对称,
∴  ,即
,即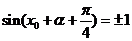 ,
,
∴ 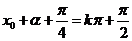 ,即
,即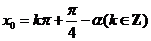 (4分) ∴
(4分) ∴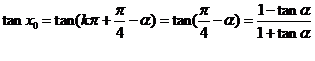 (6分)
(6分)
 .
(8分)
.
(8分)
7 (闵行区2008学年第一学期高三质量监控数学文卷第19题)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知角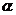 的顶点在原点,始边与
的顶点在原点,始边与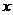 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点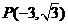 .
.
(1)求行列式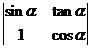 的值;
的值;
(2)若函数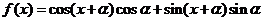 (
(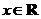 ),
),
求函数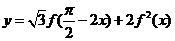 的最大值,并指出取到最大值时
的最大值,并指出取到最大值时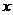 的值.
的值.
答案:(1) 角
角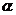 终边经过点
终边经过点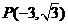 ,
,
∴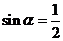 ,
,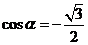 ,
, .
(3分)
.
(3分)
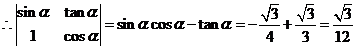 (6分)
(6分)
(2)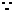
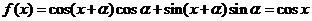 (
(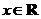 ),
(2分)
),
(2分)
∴函数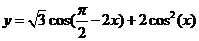
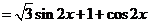
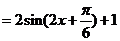 (
(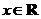 ),
(4分)
),
(4分)
∴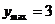 , (6分)
此时
, (6分)
此时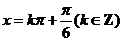 . (8分)
. (8分)
8 (南汇区2008学年度第一学期期末理科第17题)(本题满分14分)
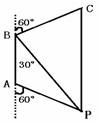 某轮船以30海里/时的速度航行,在A点测得海面上油井P在南偏东60°,向北航行40分钟后到达B点,测得油井P在南偏东30°,轮船改为北偏东60°的航向再行驶80分钟到达C点,求P、C间的距离。
某轮船以30海里/时的速度航行,在A点测得海面上油井P在南偏东60°,向北航行40分钟后到达B点,测得油井P在南偏东30°,轮船改为北偏东60°的航向再行驶80分钟到达C点,求P、C间的距离。
答案:解:如图,在△ABP中,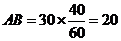 ,∠APB=30°,∠BAP=120°
,∠APB=30°,∠BAP=120°
由正弦定理知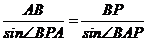 得
得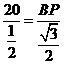 ∴
∴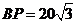 ……………………6分
……………………6分
在△BPC中,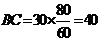 ,又∠PBC=90°∴
,又∠PBC=90°∴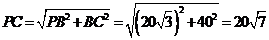
∴可得P、C间距离为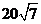 (海里) ……………………………………………………14分
(海里) ……………………………………………………14分
9. (浦东新区2008学年度第一学期期末质量抽测卷数学理科第19题)(满分14分)本题共有2小题,第1小题满分6分,第2小题满分8分.
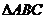 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为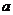 、
、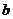 、
、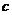 ,若
,若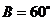 ,
, 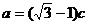 .
.
(1)求角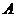 的大小;
的大小;
(2)已知当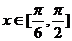 时,函数
时,函数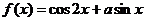 的最大值为3,求
的最大值为3,求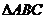 的面积.
的面积.
答案:[解](1)因为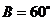 ,所以
,所以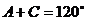 ,
, 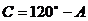 ………………1分
………………1分
因为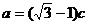 ,由正弦定理可得:
,由正弦定理可得: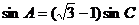 ………………3分
………………3分
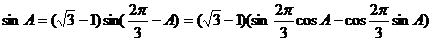
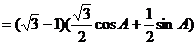 ,整理可得:
,整理可得: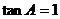 ………………5分
………………5分
所以,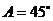 (或
(或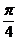 )
………………6分
)
………………6分
(2) ,令
,令 ,因为
,因为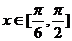 ,所以
,所以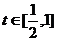 7分
7分
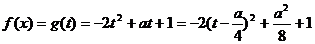 ,
,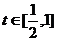 ………………9分
………………9分
若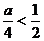 ,即
,即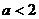 ,
,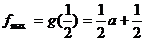 ,
,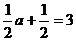 ,则
,则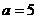 (舍去)…… 10分
(舍去)…… 10分
若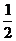
 ,即
,即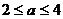 ,
,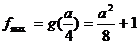 ,
,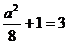 ,得
,得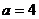 …… 11分
…… 11分
若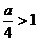 ,即
,即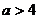 ,
, 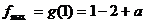
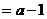 ,
, ,得
,得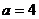 (舍去)12分
(舍去)12分
故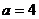 ,
,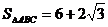 ………………14分
………………14分
9. (上海市青浦区2008学年高三年级第一次质量调研第3题)若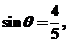 则
则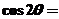 ___________.
___________.
答案: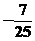
10(上海市青浦区2008学年高三年级第一次质量调研第10题)设函数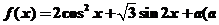 为实常数)在区间
为实常数)在区间 上的最小值为
上的最小值为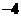 ,那么
,那么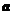 的值为__________.答案:
的值为__________.答案: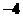
16.(上海市奉贤区2008年高三数学联考10)对于函数f(x)=x·sinx,给出下列三个命题:①f(x)是偶函数;②f(x)是周期函数;③f(x) 在区间[0,π]上的最大值为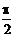 .正确的是_______________(写出所有真命题的序号).
.正确的是_______________(写出所有真命题的序号).
答案:①
1嘉定区2008-2009第一次质量调研第2题)若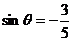 ,则行列式
,则行列式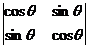 的值是______________ .答案:
的值是______________ .答案: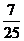
2 (嘉定区2008-2009第一次质量调研第5题)函数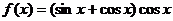 (
(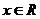 )的最小正周期为_______________.答案:
)的最小正周期为_______________.答案: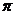
3(上海徐汇等区第一学期期末质量抽查第5题)
在△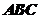 中,角
中,角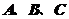 所对的边分别为
所对的边分别为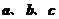 ,若
,若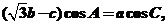 则
则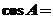 ____________.答案:
____________.答案: 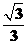
4(上海徐汇等区第一学期期末质量抽查第11题)若函数 存在反函数
存在反函数 ,且函数
,且函数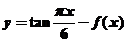 的图像过点
的图像过点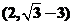 ,则函数
,则函数 的图像一定过点 ___________.
的图像一定过点 ___________.
答案: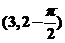
5 (2008学年度第一学期上海市普陀区高三年级质量调研第6题) 已知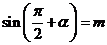 ,则
,则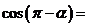 . 答案:
. 答案: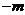
6(闸北区09届高三数学(理)第7题)若动直线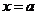 与函数
与函数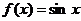 和
和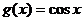 的图像分别交于
的图像分别交于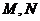 两点,则
两点,则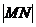 的最大值为 .
的最大值为 .
答案: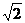 ;
;
7 (南汇区2008学年度第一学期期末理科第4题)已知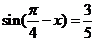 ,则
,则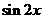 = .
= .
答案: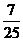
8 (浦东新区2008学年度第一学期期末质量抽测卷数学理科第6题)函数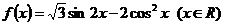 的最小正周期为
.答案:
的最小正周期为
.答案: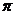
15.(上海市奉贤区2008年高三数学联考7)已知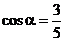 ,且
,且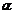 是第四象限的角,则
是第四象限的角,则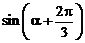 =_________________.
=_________________.
答案: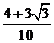
14.( 2009年上海市普通高等学校春季招生考试8)在△ 中,若
中,若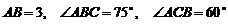 ,则
,则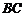 等于
.
等于
.
答案: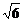 .
.
13. (上海市黄浦区2008学年高三年级第一次质量调研13)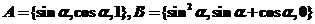 ,且
,且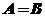 ,则
,则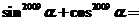 (
)
(
)
A.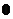 B.
B.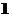 C.
C.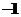 D.
D.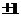
答案:C
12.(上海市黄浦区2008学年高三年级第一次质量调研5)三角方程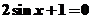 的解集是_____________.
的解集是_____________.
答案: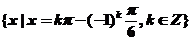 (只要正确,允许没有化简)
(只要正确,允许没有化简)
11.(上海市长宁区2008学年高三年级第一次质量调研3)函数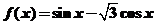 的单调递增区间为______________.
的单调递增区间为______________.
答案: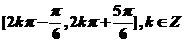
10.(上海市八校2008学年第一学期高三数学考试试卷3)函数 的递增区间
的递增区间
答案: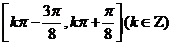
9.(08年上海市部分重点中学高三联考7)已知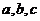 是锐角
是锐角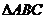 中
中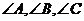 的对边,若
的对边,若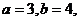
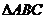 的面积为
的面积为 ,
,
则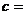
答案: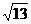
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com