
12、(2009广东潮州)已知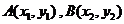 是
是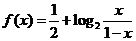 的图象上任意两点,设点
的图象上任意两点,设点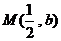 ,
,
且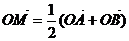 ,若
,若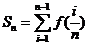 ,其中
,其中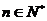 ,且
,且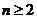 。
。
(1)求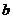 的值; (2)求
的值; (2)求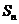 ;
;
(3)数列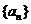 中
中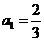 ,当
,当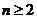 时,
时,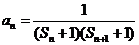 ,设数列
,设数列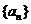 的前
的前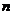 项和为
项和为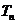 ,
,
求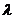 的取值范围使
的取值范围使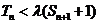 对一切
对一切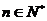 都成立。
都成立。
11、(2009广东揭阳)已知函数 ,函数
,函数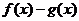 其中一个零点为5,数列
其中一个零点为5,数列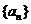 满足
满足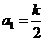 ,且
,且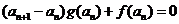 .
.
(1)求数列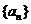 通项公式;
通项公式;
(2)试证明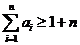 ;
;
(3)设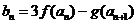 ,试探究数列
,试探究数列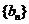 是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.
是否存在最大项和最小项?若存在求出最大项和最小项,若不存在,说明理由.
10、(2009广东揭阳)已知向量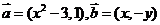 ,(其中实数
,(其中实数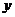 和
和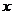 不同时为零),当
不同时为零),当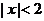 时,有
时,有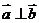 ,当
,当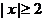 时,
时,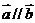 .
.
(1) 求函数式 ;
;
(2)求函数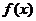 的单调递减区间;
的单调递减区间;
(3)若对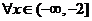
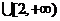 ,都有
,都有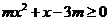 ,求实数
,求实数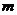 的取值范围.
的取值范围.
9、(2009广东深圳)若定义在R上的函数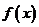 对任意的
对任意的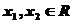 ,都有
,都有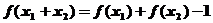 成立,且当
成立,且当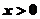 时,
时,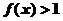 。
。
(1)求证: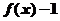 为奇函数;
为奇函数;
(2)求证: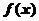 是R上的增函数;
是R上的增函数;
(3)若 ,解不等式
,解不等式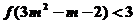 .
.
8、(2009广州(一)已知二次函数 ,其中
,其中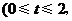 t为常数);
t为常数); 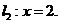 若直线l1、l2与函数f (x)的图象以及l1,y轴与函数f (x)的图象所围成的封闭图形如阴影所示.
若直线l1、l2与函数f (x)的图象以及l1,y轴与函数f (x)的图象所围成的封闭图形如阴影所示.
(Ⅰ)根据图象求a、b、c的值;
(Ⅱ)求阴影面积S关于t的函数S(t)的解析式;
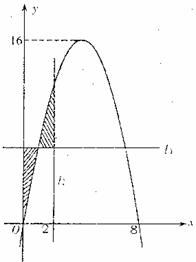
(Ⅲ)若 问是否存在实数m, 使得y=f (x)的图象与y=g (x)的图象有且只有两个不同的交点? 若存在,求出m的值;
问是否存在实数m, 使得y=f (x)的图象与y=g (x)的图象有且只有两个不同的交点? 若存在,求出m的值;
 若不存在,说明理由.
若不存在,说明理由.
7、(2009广东湛江)已知函数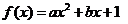 (
(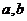 为实数),
为实数),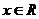 ,
,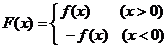 .
.
(1)若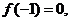 且函数
且函数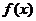 的值域为
的值域为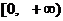 ,求
,求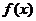 的表达式;
的表达式;
(2)在(1)的条件下,当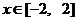 时,
时,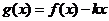 是单调函数,求实数k的取值
是单调函数,求实数k的取值
范围;
(3)设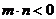 ,
,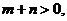
 且
且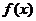 为偶函数,判断
为偶函数,判断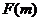 +
+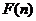 能否大于零.
能否大于零.
6、(2009广州海珠)已知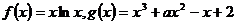
(Ⅰ)求函数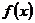 的单调区间;
的单调区间;
(Ⅱ)求函数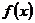 在
在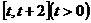 上的最小值;
上的最小值;
(Ⅲ)对一切的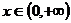 ,
,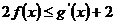 恒成立,求实数
恒成立,求实数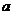 的取值范围.
的取值范围.
5、(2009广东东莞)已知函数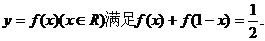
(Ⅰ)求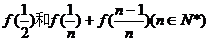 的值;
的值;
(Ⅱ)若数列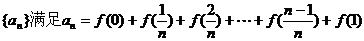 ,求列数
,求列数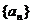 的通项公式;
的通项公式;
(Ⅲ)若数列{bn}满足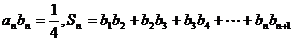 ,则实数k为何值时,不等式
,则实数k为何值时,不等式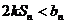 恒成立.
恒成立.
4、(2009广东东莞)已知函数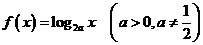 ,
,
(1)若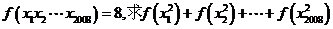 的值.
的值.
(2)当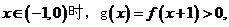 求a的取值范围.
求a的取值范围.
(3)若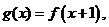 当动点
当动点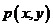 在
在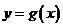 的图象上运动时,点
的图象上运动时,点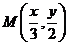 在函数
在函数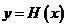 的图象上运动,求
的图象上运动,求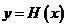 的解析式.
的解析式.
3、(2009广东揭阳)已知二次函数 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为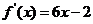 ,数列
,数列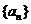 的前n项和为
的前n项和为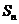 ,点
,点 均在函数
均在函数 的图像上。
的图像上。
(Ⅰ)、求数列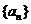 的通项公式; (Ⅱ)、设
的通项公式; (Ⅱ)、设 ,
,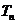 是数列
是数列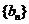 的前n项和,求使得
的前n项和,求使得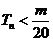 对所有
对所有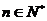 都成立的最小正整数m。
都成立的最小正整数m。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com