
35.设直线方程时,一般可设直线的斜率为k,你是否注意到直线垂直于x轴时,斜率k不存在的情况?(例如:一条直线经过点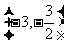 ,且被圆
,且被圆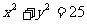 截得的弦长为8,求此弦所在直线的方程。该题就要注意,不要漏掉x+3=0这一解.)
截得的弦长为8,求此弦所在直线的方程。该题就要注意,不要漏掉x+3=0这一解.)
34.直线方程的几种形式:点斜式、斜截式、两点式、截矩式、一般式.以及各种形式的局限性,(如点斜式不适用于斜率不存在的直线,所以设方程的点斜式或斜截式时,就应该先考虑斜率不存在的情形)。
33.教材中“直线和圆”与“圆锥曲线”两章内容体现出解析几何的本质是用代数的方法研究图形的几何性质。(即数形结合)(04上海高考试题)
32.平面图形的翻折、立体图形的展开等一类问题,要注意翻折、展开前后有关几何元素的“不变量”与“不变性”。
31.面积射影定理 ,其中
,其中 表示射影面积,
表示射影面积,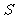 表示原面积。
表示原面积。
30.作出二面角的平面角主要方法是什么(定义法、三垂线定理法、垂面法)
29.求点到面的距离的常规方法是什么?(直接法、体积变换法、向量法)
28.棱体的顶点在底面的射影何时为底面的内心、外心、垂心、重心?
27.异面直线所成角利用“平移法”求解时,一定要注意平移后所得角是所求角或其补角。
26.立体几何中常用一些结论:棱长为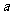 的正四面体的高为
的正四面体的高为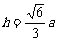 ,体积为V=
,体积为V=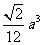 ,内切球的半径为
,内切球的半径为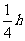 ,外切球的半径为
,外切球的半径为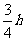 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com