
6. 如图所示,S1、S2是两个相干波源,它们振动同步且振幅相同。实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷。关于图中所标的a、b、c、d四点,下列说法中正确的有( )
如图所示,S1、S2是两个相干波源,它们振动同步且振幅相同。实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷。关于图中所标的a、b、c、d四点,下列说法中正确的有( )
A.该时刻a质点振动最弱,b、c质点振动最强,d质点振
动既不是最强也不是最弱
B.该时刻a质点振动最弱,b、c、d质点振动都最强
C.a质点的振动始终是最弱的, b、c、d质点的振动始终是最强的
D.再过T/4后的时刻a、b、c三个质点都将处于各自的平衡位置,因此振动最弱
5.关于电磁波和电磁场,下列叙述中正确的是( )
A.均匀变化的电场在它的周围空间产生均匀变化的磁场
B.电磁波中每一处的电场强度和磁感应强度总是互相垂直的,且与波的传播方向垂直
C.电磁波和机械波一样依赖于介质传播
D.只要空间某个区域有振荡的电场或磁场,就能产生电磁波
4.A、B两列波在某时刻的波形如图所示,经过t=TA时间(TA为波A的周期),两波再次出现如图波形,则两波的波速之比vA:vB可能是( )
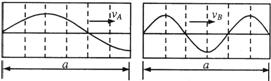 A.1:3 B.1:2
A.1:3 B.1:2
C.2:1 D.3:1
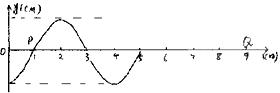
3.图示表示一列简谐波沿x轴正方向传播在t=0时的波形图,已知这列波在P点依次出现2个波峰的时间间隔为0.4s,则下列说法中正确的是:( )
A.这列波的波长是5m
B.这列波的波速是10m/s
C.质点Q要再经过0.7s才能第一次到达波峰处
D.质点Q到达波峰时,质点P也恰好达到波峰处
2.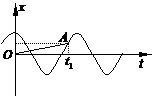 一个质点做简谐运动,它的振动图象如图,则(
)
一个质点做简谐运动,它的振动图象如图,则(
)
A.图中的曲线部分是质点的运动轨迹
B.有向线段OA是质点在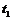 时间内的位移
时间内的位移
C.有向线段OA在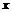 轴的投影是质点在
轴的投影是质点在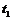 时间内的位移
时间内的位移
D.有向线段OA的斜率是质点在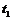 时刻的瞬时速率
时刻的瞬时速率
1.一个在水平方向做简谐运动的弹簧振子的振动周期是0.4s,当振子从平衡位置开始向右运动,在0.05s时刻,振子的运动情况是( )
A.正在向左做减速运动 B.正在向右做加速运动
C.加速度正在减小 D.动能正在减小
20.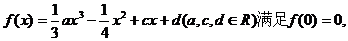 已知函数
已知函数
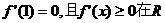 上恒成立
上恒成立
(1)求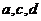 的值;
的值;
(2)若
(3)是否存在实数m,使函数 上有最小值-5?若
上有最小值-5?若
存在,请求出实数m的值;若不存在,请说明理由.
解:(1)
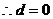
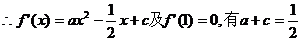
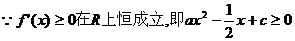 恒成立
恒成立
即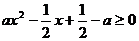 恒成立
恒成立
显然 时,上式不能恒成立
时,上式不能恒成立
 是二次函数
是二次函数
由于对一切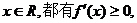 于是由二次函数的性质可得
于是由二次函数的性质可得
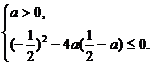 即
即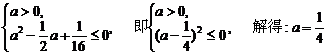
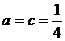 .
.
(2)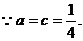
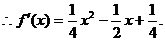
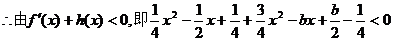
即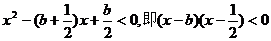
当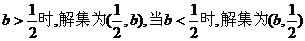 ,当
,当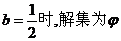 .
.
(3)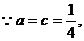
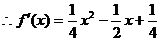
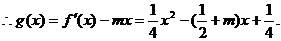
该函数图象开口向上,且对称轴为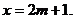
假设存在实数m使函数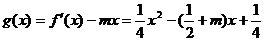 区间
区间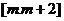 上有
上有
最小值-5.
①当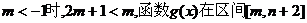 上是递增的.
上是递增的.
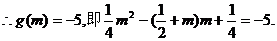
解得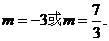
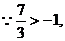
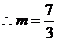 舍去
舍去
②当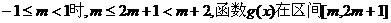 上是递减的,而在
上是递减的,而在
区间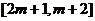 上是递增的,
上是递增的,
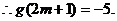
即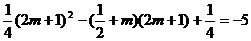
解得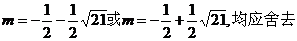
③当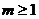 时,
时,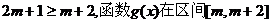 上递减的
上递减的
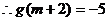
即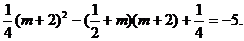
解得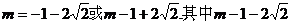 应舍去.
应舍去.
综上可得,当 时,
时,
函数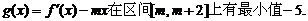
19.数列{an}满足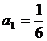 ,前n项和
,前n项和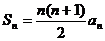 ,
,
(1)写出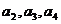
(2)猜出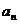 ,并用数学归纳法证明。
,并用数学归纳法证明。
解:(1)由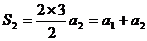 得:
得: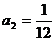
由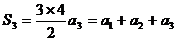 得:
得: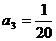
由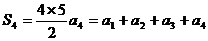 得:
得: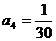
(2)猜想: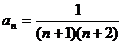
证明:①当n=1时,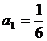 ,
,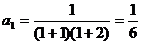 ,等式成立。
,等式成立。
②假设当n=k时等式成立,则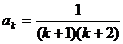 ,当n=k+1时,
,当n=k+1时,
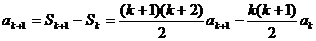
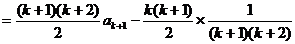
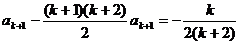
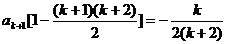
 ,综合①②,等式成立。
,综合①②,等式成立。
17.一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为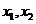 ,记
,记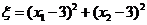 .
.
(1)分别求出 取得最大值和最小值时的概率;
取得最大值和最小值时的概率;
(2)求 的分布列及数学期望.
的分布列及数学期望.
解:(1)掷出点数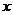 可能是:
可能是: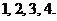
则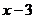 分别得:
分别得: 于是
于是 的所有取值分别为:
的所有取值分别为: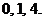
因此 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
当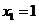 且
且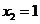 时,
时,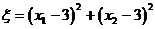 可取得最大值
可取得最大值 ,
,
此时,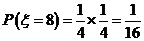 ;
;
当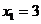 且
且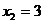 时,
时,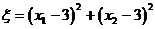 可取得最小值
可取得最小值 .
.
此时,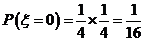 .
.
(2)由(Ⅰ)知 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
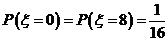 ;
;
当 =1时,
=1时,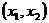 的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即
的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即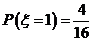 ;
;
当 =2时,
=2时,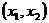 的所有取值为(2,2)、(4,4)、(4,2)、(2,4).
的所有取值为(2,2)、(4,4)、(4,2)、(2,4).
即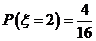 ;
;
当 =4时,
=4时,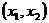 的所有取值为(1,3)、(3,1).即
的所有取值为(1,3)、(3,1).即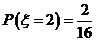 ;
;
当 =5时,
=5时,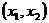 的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即
的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即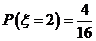 .
.
所以ξ的分布列为:
|
ξ |
0 |
1 |
2 |
4 |
5 |
8 |
|
P |
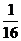 |
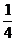 |
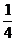 |
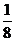 |
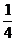 |
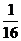 |
18
已知函数 .
.
(Ⅰ)若函数 在
在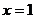 处取得极值,且曲线
处取得极值,且曲线 在点
在点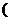
 ,
,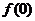
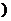 处的切线与直线
处的切线与直线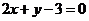 平行,求
平行,求 的值;
的值;
(Ⅱ)若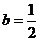 ,试讨论函数
,试讨论函数 的单调性.
的单调性.
解:(Ⅰ)函数 的定义域为
的定义域为 .
.

由题意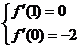 ,解得
,解得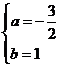
 .
.
(Ⅱ)若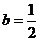 , 则
, 则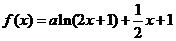 .
.
 .
.
(1)令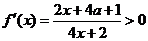 ,由函数定义域可知,
,由函数定义域可知, ,所以
,所以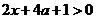
①当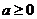 时,
时, ,
,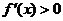 ,函数
,函数 单调递增;
单调递增;
②当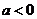 时,
时,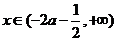 ,
,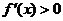 ,函数
,函数 单调递增;
单调递增;
(2)令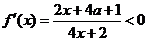 ,即
,即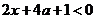
①当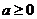 时,不等式
时,不等式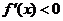 无解;
无解;
②当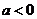 时,
时,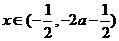 ,
,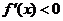 ,函数
,函数 单调递减;
单调递减;
综上:当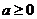 时,函数
时,函数 在区间
在区间 为增函数;
为增函数;
当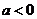 时,函数
时,函数 在区间
在区间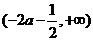 为增函数;
为增函数;
在区间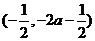 为减函数.
为减函数.
16. 在三棱锥
在三棱锥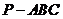 中,
中,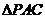 和
和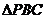 是边长为
是边长为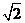 的等边三角形,
的等边三角形,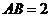 ,
, 是
是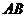 中点.
中点.
(Ⅰ)在棱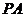 上求一点
上求一点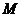 ,使得
,使得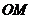 ∥平面
∥平面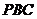 ;
;
(Ⅱ)求证:平面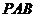 ⊥平面
⊥平面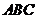 ;
;
(Ⅲ)求二面角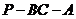 的余弦值.
的余弦值.
解
(Ⅰ)当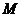 为棱
为棱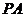 中点时,
中点时,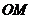 ∥平面
∥平面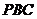 .
.
证明如下:
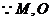 分别为
分别为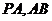 中点,
中点,
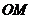 ∥
∥
又 平面
平面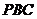 ,
,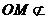 平面
平面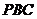
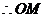 ∥平面
∥平面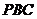 .
.
(Ⅱ)连结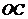 ,
,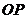
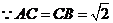 ,
,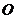 为
为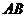 中点,
中点,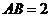 ,
,
 ⊥
⊥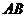 ,
,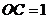 .
.
同理, 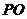 ⊥
⊥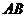 ,
,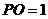 .
.
 又
又 ,
,
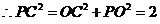 ,
,
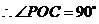 .
.
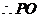 ⊥
⊥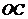 .
.

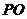 ⊥
⊥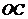 ,
,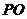 ⊥
⊥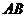 ,
,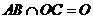 ,
,
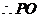 ⊥平面
⊥平面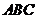 .
.
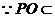 平面
平面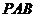
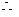 平面
平面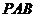 ⊥平面
⊥平面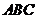 .
.
(Ⅲ)如图,建立空间直角坐标系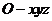 .
.
则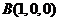 ,
,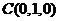 ,
,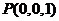 ,
,
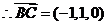 ,
,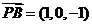 .
.
由(Ⅱ)知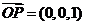 是平面
是平面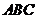
的一个法向量.
设平面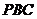 的法向量为
的法向量为 ,
,
则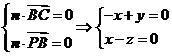 .
.
令 ,则
,则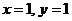 ,
,
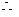 平面
平面 的一个法向量
的一个法向量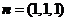 .
.
 .
.
 二面角
二面角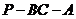 的平面角为锐角,
的平面角为锐角,
 所求二面角
所求二面角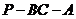 的余弦值为
的余弦值为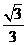 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com