
21.(2001江西、山西、天津理)如图5-6,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC的中点,正四棱锥底面边长为2a,高为h.
(1)求cos<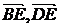 >;
>;
(2)记面BCV为α,面DCV为β,若∠BED是二面角α-VC-β的平面角,求∠BED.
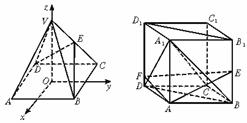
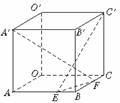
图5-6 图5-7 图5-8
20.(2002天津文22,理21)已知两点M(-1,0),N(1,0),且点P使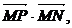
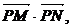
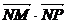 成公差小于零的等差数列.
成公差小于零的等差数列.
(1)点P的轨迹是什么曲线?
(2)若点P坐标为(x0,y0),θ为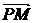 与
与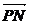 的夹角,求tanθ.
的夹角,求tanθ.
19.(2002天津文9,理18)如图5-5,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为 a.
a.
(1)建立适当的坐标系,并写出点A、B、A1、C1的坐标;
(2)求AC1与侧面ABB1A1所成的角.
18.(2002上海,17)如图5-4,在直三棱柱ABO-A′B′O′中,OO′=4,OA=4,OB=3,∠AOB=90°,D是线段A′B′的中点,P是侧棱BB′上的一点,若OP⊥BD,求OP与底面AOB所成角的大小.(结果用反三角函数值表示)
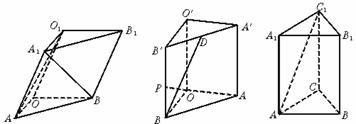
图5-3 图5-4 图5-5
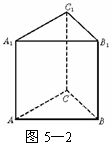 16.(2003上海春,19)已知三棱柱ABC-A1B1C1,在某个空间直角坐标系中,
16.(2003上海春,19)已知三棱柱ABC-A1B1C1,在某个空间直角坐标系中,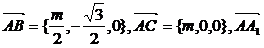 ={0,0,n}.(其中m、n>0).如图5-2.
={0,0,n}.(其中m、n>0).如图5-2.
(1)证明:三棱柱ABC-A1B1C1是正三棱柱;
(2)若m= n,求直线CA1与平面A1ABB1所成角的大小.
n,求直线CA1与平面A1ABB1所成角的大小.
17.(2002上海春,19)如图5-3,三棱柱OAB-O1A1B1,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=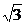 .求:
.求:
(1)二面角O1-AB-O的大小;
(2)异面直线A1B与AO1所成角的大小.
(上述结果用反三角函数值表示)
15.(1996上海,15)已知O(0,0)和A(6,3)两点,若点P在直线OA上,且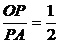 ,又P是线段OB的中点,则点B的坐标是_____.
,又P是线段OB的中点,则点B的坐标是_____.
14.(1996上海,15)已知a+b=2i-8j,a-b=-8i+16j,那么a·b=_____.
13.(1997上海,14)设a=(m+1)i-3j,b=i+(m-1)j,(a+b)⊥(a-b),则m=_____.
12.(1999上海理,8)若将向量a=(2,1)围绕原点按逆时针方向旋转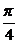 得到向量b,则向量b的坐标为_____.
得到向量b,则向量b的坐标为_____.
11.(2000上海,1)已知向量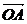 =(-1,2),
=(-1,2), =(3,m),若
=(3,m),若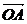 ⊥
⊥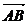 ,则m= .
,则m= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com