
12.答案:( )
)
解析:设a= =2+i,b=
=2+i,b= ,由已知
,由已知 、
、 的夹角为
的夹角为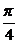 ,由复数乘法的几何意义,得
,由复数乘法的几何意义,得 =
= (cos
(cos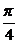 +isin
+isin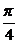 )=(2+i)
)=(2+i) .
.
∴b=( )
)
评述:本题考查向量的概念,向量与复数一一对应关系,考查变通、变换等数学方法,以及运用数学知识解决问题的能力.
11.答案:4
解析:∵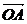 ={-1,2},
={-1,2}, ={3,m},
={3,m}, ={4,m-2},又
={4,m-2},又 ⊥
⊥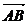 ,
,
∴-1×4+2(m-2)=0,∴m=4.
评述:本题考查向量的概念,向量的运算,向量的数量积及两向量垂直的充要条件.
10.答案:90°
解析:由|α+β|=|α-β|,可画出几何图形,如图5-14.
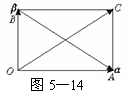 |α-β|表示的是线段AB的长度,|α+β|表示线段OC的长度,由|AB|=|OC|
|α-β|表示的是线段AB的长度,|α+β|表示线段OC的长度,由|AB|=|OC|
∴平行四边形OACB为矩形,故向量α与β所成的角为90°
评述:本题考查向量的概念,向量的几何意义,向量的运算.这些知识不只在学习向量时用到,而且在复数、物理学中也是一些最基本的知识.
9.答案:13
解析:∵(2a-b)·a=2a2-b·a=2|a|2-|a|·|b|·cos120°=2·4-2·5(-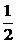 )=13.
)=13.
评述:本题考查向量的运算关系.
8.答案:A
解析:设直线l的方程为y=kx+b(此题k必存在),则直线向左平移3个单位,向上平移1个单位后,直线方程应为y=k(x+3)+b+1即y=kx+3k+b+1
因为此直线与原直线重合,所以两方程相同.比较常数项得3k+b+1=b.∴k=- .
.
评述:本题考查平移变换与函数解析式的相互关系.
7.答案:D
解析:①平面向量的数量积不满足结合律.故①假;
②由向量的减法运算可知|a|、|b|、|a-b|恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;
③因为[(b·c)a-(c·a)b]·c=(b·c)a·c-(c·a)b·c=0,所以垂直.故③假;
④(3a+2b)(3a-2b)=9·a·a-4b·b=9|a|2-4|b|2成立.故④真.
评述:本题考查平面向量的数量积及运算律.
6.答案:B
解析:设c=ma+nb,则(-1,2)=m(1,1)+n(1,-1)=(m+n,m-n).
∴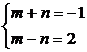 ∴
∴
评述:本题考查平面向量的表示及运算.
5.答案:A
解析: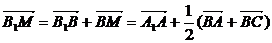 =c+
=c+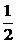 (-a+b)=-
(-a+b)=-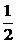 a+
a+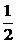 b+c
b+c
评述:用向量的方法处理立体几何问题,使复杂的线面空间关系代数化,本题考查的是基本的向量相等,与向量的加法.考查学生的空间想象能力.
4.答案:B
解法一:设A(x1,y1),B(x2,y2),AB所在直线方程为y=k(x-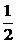 ),则
),则 =x1x2+y1y2.又
=x1x2+y1y2.又 ,得k2x2-(k2+2)x+
,得k2x2-(k2+2)x+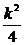 =0,∴x1·x2=
=0,∴x1·x2=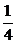 ,而y1y2=k(x1-
,而y1y2=k(x1-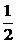 )k(x2-
)k(x2-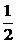 )=k2(x1-
)=k2(x1-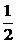 )(x2-
)(x2-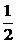 )=-1.∴x1x2+y1y2=
)=-1.∴x1x2+y1y2=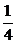 -1=-
-1=- .
.
解法二:因为直线AB是过焦点的弦,所以y1·y2=-p2=-1.x1·x2同上.
评述:本题考查向量的坐标运算,及数形结合的数学思想.
3.答案:D
解析:设(x,y)=2b-a=2(0,-1)-(3,2)=(-3,-4).
评述:考查向量的坐标表示法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com