
3.向量在空间中的应用(在B类教材中).在空间坐标系下,通过向量的坐标的表示,运用计算的方法研究三维空间几何图形的性质.
在复习过程中,抓住源于课本,高于课本的指导方针.本章考题大多数是课本的变式题,即源于课本.因此,掌握双基、精通课本是本章关键.
2.以解答题考查圆锥曲线中的典型问题.此类题综合性比较强,难度大,以解析几何中的常规题为主.
1.以选择、填空题型考查本章的基本概念和性质.此类题一般难度不大,用以解决有关长度、夹角、垂直、判断多边形形状等问题.
29.解:(1)过D作DE⊥BC,垂足为E,在Rt△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,得BD=1,CD=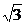 ,∴DE=CD·sin30°=
,∴DE=CD·sin30°=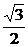 .
.
OE=OB-BE=OB-BD·cos60°=1-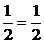 .
.
∴D点坐标为(0,-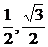 ),即向量OD[TX→]的坐标为{0,-
),即向量OD[TX→]的坐标为{0,-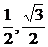 }.
}.
(2)依题意: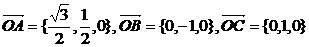 ,
,
所以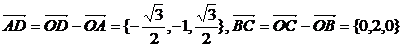 .
.
设向量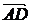 和
和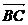 的夹角为θ,则
的夹角为θ,则
cosθ=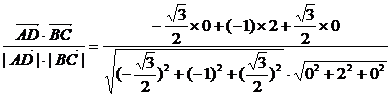
 .
.
评述:本题考查空间向量坐标的概念,空间向量数量积的运算及空间向量的夹角公式.解决好本题的关键是对空间向量坐标的概念理解清楚,计算公式准确,同时还要具备很好的运算能力.
●命题趋向与应试策略
对本章内容的考查主要分以下三类:
28.(1)证明:∵PA⊥平面ABCD,∴PA⊥AB,又AB⊥AD.∴AB⊥平面PAD.又∵AE⊥PD,∴PD⊥平面ABE,故BE⊥PD.
(2)解:以A为原点,AB、AD、AP所在直线为坐标轴,建立空间直角坐标系,则点C、D的坐标分别为(a,a,0),(0,2a,0).
∵PA⊥平面ABCD,∠PDA是PD与底面ABCD所成的角,∴∠PDA=30°.
于是,在Rt△AED中,由AD=2a,得AE=a.过E作EF⊥AD,垂足为F,在Rt△AFE中,由AE=a,∠EAF=60°,得AF= ,EF=
,EF=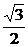 a,∴E(0,
a,∴E(0,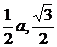 a)
a)
于是,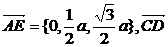 ={-a,a,0}
={-a,a,0}
设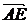 与
与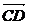 的夹角为θ,则由cosθ=
的夹角为θ,则由cosθ=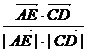
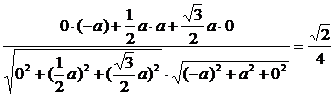
∴θ=arccos ,即AE与CD所成角的大小为arccos
,即AE与CD所成角的大小为arccos .
.
评述:第(2)小题中,以向量为工具,利用空间向量坐标及数量积,求两异面直线所成的角是立体几何中的常见问题和处理手段.
27.(1)证明:设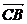 =a,
=a,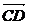 =b,
=b,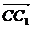 =c,则|a|=|b|,∵
=c,则|a|=|b|,∵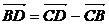 =b-a,
=b-a,
∴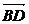 ·
·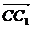 =(b-a)·c=b·c-a·c=|b|·|c|cos60°-|a|·|c|cos60°=0,
=(b-a)·c=b·c-a·c=|b|·|c|cos60°-|a|·|c|cos60°=0,
∴C1C⊥BD.
(2)解:连AC、BD,设AC∩BD=O,连OC1,则∠C1OC为二面角α-BD-β的平面角.
∵ (a+b),
(a+b),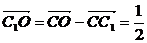 (a+b)-c
(a+b)-c
∴ ·
· (a+b)·[
(a+b)·[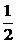 (a+b)-c]
(a+b)-c]
= (a2+2a·b+b2)-
(a2+2a·b+b2)-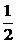 a·c-
a·c-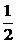 b·c
b·c
= (4+2·2·2cos60°+4)-
(4+2·2·2cos60°+4)-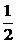 ·2·
·2·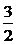 cos60°-
cos60°-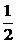 ·2·
·2·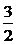 cos60°=
cos60°=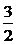 .
.
则| |=
|=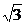 ,|
,| |=
|=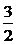 ,∴cosC1OC=
,∴cosC1OC=
(3)解:设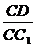 =x,CD=2,
则CC1=
=x,CD=2,
则CC1=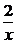 .
.
∵BD⊥平面AA1C1C,∴BD⊥A1C
∴只须求满足: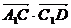 =0即可.
=0即可.
设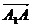 =a,
=a,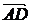 =b,
=b,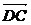 =c,
=c,
∵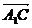 =a+b+c,
=a+b+c,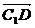 =a-c,
=a-c,
∴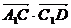 =(a+b+c)(a-c)=a2+a·b-b·c-c2=
=(a+b+c)(a-c)=a2+a·b-b·c-c2=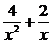 -6,令6-
-6,令6- =0,得x=1或x=-
=0,得x=1或x=-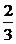 (舍去).
(舍去).
评述:本题蕴涵着转化思想,即用向量这个工具来研究空间垂直关系的判定、二面角的求解以及待定值的探求等问题.
26.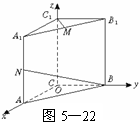 解:如图5-22,建立空间直角坐标系O-xyz.
解:如图5-22,建立空间直角坐标系O-xyz.
(1)依题意得B(0,1,0)、N(1,0,1)
∴|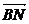 |=
|= .
.
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴ ={-1,-1,2},
={-1,-1,2},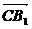 ={0,1,2,},
={0,1,2,}, ·
·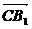 =3,|
=3,| |=
|=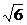 ,|
,|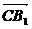 |=
|=
∴cos< ,
,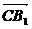 >=
>= .
.
(3)证明:依题意,得C1(0,0,2)、M(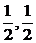 ,2),
,2),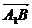 ={-1,1,2},
={-1,1,2},
 ={
={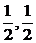 ,0}.
,0}.
∴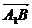 ·
· =-
=- +0=0,∴
+0=0,∴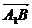 ⊥
⊥ ,∴A1B⊥C1M.
,∴A1B⊥C1M.
评述:本题主要考查空间向量的概念及运算的基本知识.考查空间两向量垂直的充要条件.
25. 解:如图5-21建立空间直角坐标系
解:如图5-21建立空间直角坐标系
由题意,有A(0,2,0)、C(2,0,0)、E(1,1,0)
设D点的坐标为(0,0,z)(z>0)
则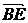 ={1,1,0},
={1,1,0},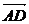 ={0,-2,z},
={0,-2,z},
设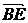 与
与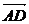 所成角为θ.
所成角为θ.
则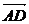 ·
·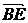 =
= ·
·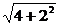 cosθ=-2,且AD与BE所成的角的大小为arccos
cosθ=-2,且AD与BE所成的角的大小为arccos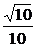 .∴cos2θ=
.∴cos2θ=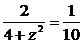 ,∴z=4,故|BD|的长度为4.
,∴z=4,故|BD|的长度为4.
又VA-BCD= |AB|×|BC|×|BD|=
|AB|×|BC|×|BD|=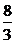 ,因此,四面体ABCD的体积为
,因此,四面体ABCD的体积为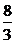 .
.
评述:本题考查空间图形的长度、角度、体积的概念和计算.以向量为工具,利用空间向量的坐标表示、空间向量的数量积计算线段的长度、异面直线所成角等问题,思路自然,解法灵活简便.
24.(1)证明:∵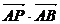 =-2-2+4=0,∴AP⊥AB.
=-2-2+4=0,∴AP⊥AB.
又∵ =-4+4+0=0,∴AP⊥AD.
=-4+4+0=0,∴AP⊥AD.
∵AB、AD是底面ABCD上的两条相交直线,∴AP⊥底面ABCD.
(2)解:设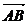 与
与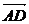 的夹角为θ,则
的夹角为θ,则
cosθ=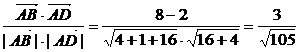
V=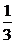 |
|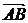 |·|
|·|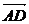 |·sinθ·|
|·sinθ·|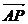 |=
|=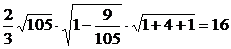
(3)解:|(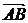 ×
×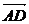 )·
)·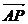 |=|-4-32-4-8|=48它是四棱锥P-ABCD体积的3倍.
|=|-4-32-4-8|=48它是四棱锥P-ABCD体积的3倍.
猜测:|(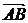 ×
×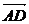 )·
)·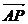 |在几何上可表示以AB、AD、AP为棱的平行六面体的体积(或以AB、AD、AP为棱的直四棱柱的体积).
|在几何上可表示以AB、AD、AP为棱的平行六面体的体积(或以AB、AD、AP为棱的直四棱柱的体积).
评述:本题考查了空间向量的坐标表示、空间向量的数量积、空间向量垂直的充要条件、空间向量的夹角公式和直线与平面垂直的判定定理、棱锥的体积公式等.主要考查考生的运算能力,综合运用所学知识解决问题的能力及空间想象能力.
23. 建立坐标系,如图5-20.
建立坐标系,如图5-20.
(1)证明:设AE=BF=x,则A′(a,0,a),F(a-x,a,0),C′(0,a,a),E(a,x,0)
∴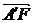 ={-x,a,-a},
={-x,a,-a}, ={a,x-a,-a}.
={a,x-a,-a}.
∵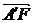 ·
· =-xa+a(x-a)+a2=0
=-xa+a(x-a)+a2=0
∴A′F⊥C′E
(2)解:设BF=x,则EB=a-x
三棱锥B′-BEF的体积
V= x(a-x)·a≤
x(a-x)·a≤ (
(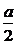 )2=
)2=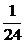 a3
a3
当且仅当x=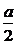 时,等号成立.
时,等号成立.
因此,三棱锥B′-BEF的体积取得最大值时BE=BF=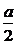 ,过B作BD⊥EF于D,连
,过B作BD⊥EF于D,连
B′D,可知B′D⊥EF.∴∠B′DB是二面角B′-EF-B的平面角在直角三角形BEF中,直角边BE=BF=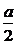 ,BD是斜边上的高.∴BD=
,BD是斜边上的高.∴BD= a.
a.
∴tanB′DB=
故二面角B′-EF-B的大小为arctan2 .
.
评述:本题考查空间向量的表示、运算及两向量垂直的充要条件.二次函数求最值或均值不等式求最值,二面角等知识.考查学生的空间想象能力和运算能力.用空间向量的观点处理立体几何中的线面关系,把几何问题代数化,降低了立体几何的难度.本题考查的线线垂直等价于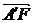 ·
· =0,使问题很容易得到解决.而体积的最值除用均值不等式外亦可用二次函数求最值的方法处理.二面角的平面角的找法是典型的三垂线定理找平面角的方法,计算较简单,有一定的思维量.
=0,使问题很容易得到解决.而体积的最值除用均值不等式外亦可用二次函数求最值的方法处理.二面角的平面角的找法是典型的三垂线定理找平面角的方法,计算较简单,有一定的思维量.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com