
2.(08浙江温州)方程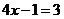 的解是( )B
的解是( )B
A.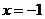 B.
B.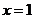 C.
C.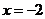 D.
D.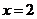
1.(2008年四川省宜宾市)小明准备为希望工程捐款,他现在有20元,以后每月打算存10元,若设x月后他能捐出100元,则下列方程中能正确计算出x的是 ( )
A. 10x+20=100 B.10x-20=100 C. 20-10x=100 D.20x+10=100
答案:A
(四)布置作业 P114⑶⑷⑸
(三)例题分析
[例题1]地球同步卫星到地心的距离r可由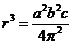 求出。已知式中
求出。已知式中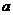 的单位是m,
的单位是m,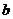 的单位是s,
的单位是s,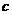 的单位是m/s2,则:
的单位是m/s2,则:
A.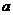 是地球半径,
是地球半径,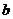 是地球自转周期,
是地球自转周期,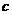 是地球表面处的重力加速度。
是地球表面处的重力加速度。
B.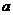 是地球半径,
是地球半径,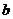 是同步卫星绕地心运动的周期,
是同步卫星绕地心运动的周期,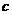 是同步卫星的加速度。
是同步卫星的加速度。
C.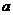 是赤道周长,
是赤道周长,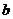 是地球自转周期,
是地球自转周期,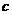 是同步卫星的加速度。
是同步卫星的加速度。
D.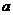 是地球半径,
是地球半径,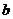 是同步卫星绕地心运动的周期,
是同步卫星绕地心运动的周期,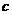 是地球表面处的重力加速度。
是地球表面处的重力加速度。
解:由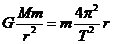 得
得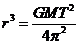 ,
,
由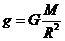 得
得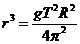 ,
,
∴A、D正确。
 [例题2]将卫星发射至近地圆轨道1(如图所示),然后再次点火,将卫星送入同步轨道3。轨道1、2相切于Q点,2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是:
[例题2]将卫星发射至近地圆轨道1(如图所示),然后再次点火,将卫星送入同步轨道3。轨道1、2相切于Q点,2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是:
A.卫星在轨道3上的速率大于轨道1上的速率。
B.卫星在轨道3上的角速度大于在轨道1上的角速度。
C.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度。
D.卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度。
解:由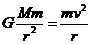 得
得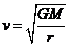 , 而
, 而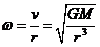 ,
,
轨道3的半径比1的大,故A错B对,“相切”隐含着切点弯曲程度相同,即卫星在切点时两轨道瞬时运行半径相同,又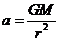 ,故C错D对。
,故C错D对。
[例题3]某星球上,宇航员用弹簧秤称得质量为m的物体重量为F,乘宇宙飞船在靠近该星球表面空间飞行,测得环绕周期为T,试求该星球的质量。
解:m物体的重量等于万有引力,设星球半径为R,飞船质量M’,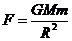 ,
,
飞船绕该星球飞行时,万有引力提供向心力:
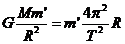 ,
,
由以上两式可得: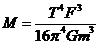
[例题4]已知地球与火星的质量之比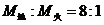 ,半径之比
,半径之比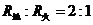 ,现用一根绳子水平拖动放在地球表面木板上的箱子,设箱子与木板动摩擦因数为0.5,在地球上拖动时,能获得10m/s2的最大加速度,将箱子、木板、绳子送到火星上,仍用同样的力和方式拖动木箱,求此木箱能获得的最大加速度。
,现用一根绳子水平拖动放在地球表面木板上的箱子,设箱子与木板动摩擦因数为0.5,在地球上拖动时,能获得10m/s2的最大加速度,将箱子、木板、绳子送到火星上,仍用同样的力和方式拖动木箱,求此木箱能获得的最大加速度。
解:地球表面: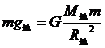 ………………①
………………①
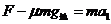 ………………②
………………②
火星表面: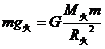 ………………③
………………③
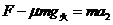 ………………④
………………④
∴以上四式联立求解得: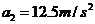
(一)复习概念规律
1.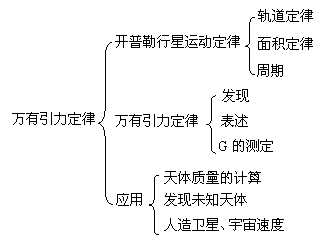 知识结构:
知识结构:
2.重点知识梳理:
(1)万有引力定律
①开普勒对行星运动规律的描述(开普勒定律)为万有引力定律的发现奠定了基础。
②万有引力定律公式:
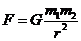 ,
,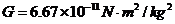
③卡文迪许用扭秤实验较准确地测定了引力常量,证明了万有引力定律的正确性。
④万有引力定律适用于一切物体,但用公式计算时,注意有一定的适用条件。
(2)万有引力定律在天文学上的应用。
①基本方法:
(i)把天体的运动看成匀速圆周运动,其所需向心力由万有引力提供: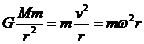
(ii)在忽略天体自转影响时,天体表面的重力加速度: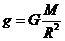 ,R为天体半径。
,R为天体半径。
②天体质量,密度的估算。
测出环绕天体作匀速圆周运动的半径r,周期为T,由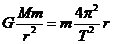 得被环绕天体的质量为
得被环绕天体的质量为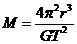 ,密度为
,密度为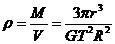 ,R为被环绕天体的半径。
,R为被环绕天体的半径。
当环绕天体在被环绕天体的表面运行时,r=R,则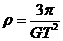 。
。
③环绕天体的绕行速度,角速度、周期与半径的关系。
(i)由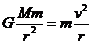 得
得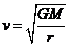
∴r越大,v越小
(ii)由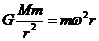 得
得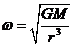
∴r越大,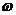 越小
越小
(iii)由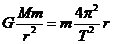 得
得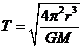
∴r越大,T越大
④三种宇宙速度
(i)第一宇宙速度(环绕速度):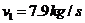 ,人造卫星的最小发射速度。
,人造卫星的最小发射速度。
(ii)第二宇宙速度(脱离速度):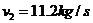 ,使物体挣脱地球束缚的最小发射速度。
,使物体挣脱地球束缚的最小发射速度。
(iii)第三宇宙速度(逃逸速度):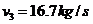 ,使物体挣脱太阳引力束缚的最小速度。
,使物体挣脱太阳引力束缚的最小速度。
⑤同步卫星:
相对于地面静止,定点在赤道正上方与地球自转有相同的周期。
2.巩固综合运用万有引力定律、圆周运动知识解决具体问题的方法。
1.归纳本章基本知识,形成知识网络。
22.(1)合金中镁的质量是4.8g,铝的质量是2.7g
(2)盐酸的物质的量浓度是8mol/L
21.w(Na2CO3)74.2% w(NaHCO3)=16.8%
w(Na2SO4)=9%
20.A:KOH B:KHCO3或KHSO3 C:K2CO3或K2SO3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com