1. 知识与技能

　　 (1)理解两个集合的并集与交集的含义，会求两个简单集合的交集与并集.

　　 (2)理解在给定集合中一个子集的补集的含义，会求给定子集的补集.

　　 (3)能使用Venn图表达集合的运算，体会直观图示对理解抽象概念的作用.

(六)布置作业

　 第13页习题 1.1A组第5题.

§1.1.3 集合的基本运算

(五)归纳整理，整体认识

　　 1．请学生回顾本节课所学过的知识内容有建些，所涉及到的主要数学思想方法又那些.

　　 2. 在本节课的学习过程中，还有那些不太明白的地方,请向老师提出.

(四)巩固深化，发展思维

　　 1. 学生在教师的引导启发下完成下列两道例题：

　　 例1．某工厂生产的产品在质量和长度上都合格时，该产品才合格。若用A表示合格产品，B表示质量合格的产品的集合,C表示长度合格的产品的集合．则下列包含关系哪些成立？

试用Venn图表示这三个集合的关系。

　　 例2　 写出集合{0，1，2)的所有子集，并指出哪些是它的真子集.

2.学生做教材第8页的练习第l-3题，教师及时检查反馈。强调能确定是真子集关系的最好写真子集，而不写子集.

(二)研探新知

投影问题2：观察下面几个例子，你能发现两个集合间有什么关系了吗？

　　 (1)；

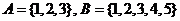　 (2)设A为国兴中学高一(3)班男生的全体组成的集合，B为这个班学生的全体组成的集合；

　　 (3)设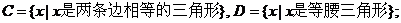

　　 (4).

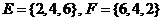　　 组织学生充分讨论.交流，使学生发现两个集合所含元素范围存在各种关系，从而类比得出两个集合之间的关系:

①一般地，对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，我们就说这两个集合有包含关系，称集合A为B的子集.

　 记作：

　 读作：A含于B(或B包含A).

　　 ②如果两个集合所含的元素完全相同，那么我们称这两个集合相等.

　　 教师引导学生类比表示集合间关系的符号与表示两个实数大小关系的等号之间有什么类似之处，强化学生对符号所表示意义的理解。并指出：为了直观地表示集合间的关系，我们常用平面上封闭曲线的内部代表集合，这种图称为Venn图。如图l和图2分别是表示问题2中实例1和实例3的Venn图.

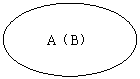
　　　　　　 图1　　　　　　　　　　　　　 图2

　　 投影问题3：与实数中的结论“若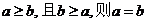”相类比，在集合中，你能得出什么结论?

　　 教师引导学生通过类比，思考得出结论: 若.

　　 问题4：请同学们举出几个具有包含关系.相等关系的集合实例，并用Venn图表示.

　　 学生主动发言，教师给予评价.

　　 (-)创设情景，揭示课题

　　 问题l：实数有相等.大小关系，如5=5，5＜7，5＞3等等，类比实数之间的关系，你会想到集合之间有什么关系呢？

　　 让学生自由发言，教师不要急于做出判断。而是继续引导学生；欲知谁正确，让我们一起来观察.研探.

2.学用具：投影仪.

1.学法：让学生通过观察.类比.思考.交流.讨论，发现集合间的基本关系.

重点：集合间的包含与相等关系，子集与其子集的概念.

难点：难点是属于关系与包含关系的区别．