1．知识与技能：

理解函数的奇偶性及其几何意义；学会运用函数图象理解和研究函数的性质；学会判断函数的奇偶性；

(五)设置问题，留下悬念

1、教师提出下列问题让学生思考：

①通过增(减)函数概念的形成过程，你学习到了什么？

②增(减)函数的图象有什么特点？如何根据图象指出单调区间？

③怎样用定义证明函数的单调性？

师生共同就上述问题进行讨论、交流，发表自己的意见。

2、书面作业：课本P₄₅习题1、3题(A组)第1-5题。

§1．3．2函数的奇偶性

(四)归纳小结

函数的单调性一般是先根据图象判断，再利用定义证明．画函数图象通常借助计算机，求函数的单调区间时必须要注意函数的定义域，单调性的证明一般分五步：

取 值 → 作 差 → 变 形 → 定 号 → 下结论

(三)质疑答辩，发展思维。

根据函数图象说明函数的单调性．

例1 如图是定义在区间[－5，5]上的函数y=f(x)，根据图象说出函数的单

调区间，以及在每一单调区间上，它是增函数还是减函数？

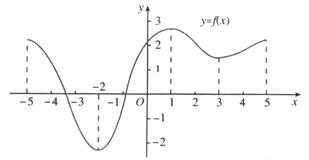
　　　 解：略

例2 物理学中的玻意耳定律P=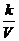(k为正常数)告诉我们，对于一定量的气体，当其体积V减少时，压强P将增大。试用函数的单调性证明之。

分析：按题意，只要证明函数P=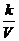在区间(0，+∞)上是减函数即可。

证明：略

3．判断函数单调性的方法步骤

　　　　　　　 利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤：

　　　　　　　 ① 任取x₁，x₂∈D，且x₁<x₂；

　　　　　　　 ② 作差f(x₁)－f(x₂)；

③变形(通常是因式分解和配方)；

④定号(即判断差f(x₁)－f(x₂)的正负)；

⑤下结论(即指出函数f(x)在给定的区间D上的单调性)．

巩固练习：

1 课本P₃₈练习第1、2、3题；

　　　 2 证明函数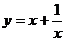在(1，+∞)上为增函数．

例3．借助计算机作出函数y =－x² +2 | x | + 3的图象并指出它的的单调区间．

解：(略)

思考：画出反比例函数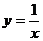的图象．

　　　 1 这个函数的定义域是什么？

　　　 2 它在定义域I上的单调性怎样？证明你的结论．

(二)研探新知

1、y = x²的图象在y轴右侧是上升的，如何用数学符号语言来描述这种“上升”呢？

学生通过观察、思考、讨论，归纳得出：

函数y = x²在(0，+∞)上图象是上升的，用函数解析式来描述就是：对于(0，+∞)上的任意的x₁，x₂，当x₁＜x₂时，都有x₁²＜x₂² . 即函数值随着自变量的增大而增大，具有这种性质的函数叫增函数。

2．增函数

一般地，设函数y=f(x)的定义域为I，

如果对于定义域I内的某个区间D内的任意两个自变量x₁，x₂，当x₁<x₂时，都有f(x₁)<f(x₂)，那么就说f(x)在区间D上是增函数(increasing function)．

3、从函数图象上可以看到，y= x²的图象在y轴左侧是下降的，类比增函数的定义，你能概括出减函数的定义吗？

注意：

1 函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质；

2 必须是对于区间D内的任意两个自变量x₁，x₂；当x₁<x₂时，总有f(x₁)<f(x₂) ．

4．函数的单调性定义

如果函数y=f(x)在某个区间上是增函数或是减函数，那么就说函数y=f(x)在这一区间具有(严格的)单调性，区间D叫做y=f(x)的单调区间：

(一)创设情景，揭示课题

1．　 观察下列各个函数的图象，并说说它们分别反映了相应函数的哪些变化规律：

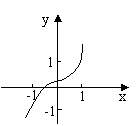
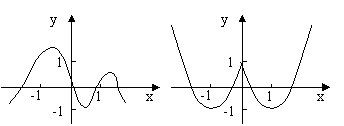
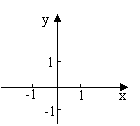1 随x的增大，y的值有什么变化？

2 能否看出函数的最大、最小值？

3 函数图象是否具有某种对称性？

2．　 画出下列函数的图象，观察其变化规律：　　　

(1)f(x) = x

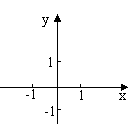　　　 1 从左至右图象上升还是下降 ______?

　　　 2 在区间 ____________ 上，随着x的增

大，f(x)的值随着 ________ ．

(2)f(x) = -x+2

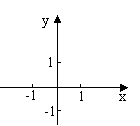　　　 1 从左至右图象上升还是下降 ______?

　　　 2 在区间 ____________ 上，随着x的增

大，f(x)的值随着 ________ ．

(3)f(x) = x²

　　　 1在区间 ____________ 上，

f(x)的值随着x的增大而 ________ ．

　　　 2 在区间 ____________ 上，f(x)的值随

着x的增大而 ________ ．

3、从上面的观察分析，能得出什么结论？

学生回答后教师归纳：从上面的观察分析可以看出：不同的函数，其图象的变

化趋势不同，同一函数在不同区间上变化趋势也不同，函数图象的这种变化规律就是函数性质的反映，这就是我们今天所要研究的函数的一个重要性质--函数的单调性(引出课题)。

2、教学用具：投影仪、计算机.

1、从观察具体函数图象引入，直观认识增减函数，利用这定义证明函数单调性。通过练习、交流反馈，巩固从而完成本节课的教学目标。

重点：函数的单调性及其几何意义．

难点：利用函数的单调性定义判断、证明函数的单调性．

3、情态与价值，使学生感到学习函数单调性的必要性与重要性，增强学习

函数的紧迫感.