
7.9 km/s,则该探月卫星绕月运行的速率约为 ( )
A.0.4 km/s B.1.8 km/s C.11 km/s D.36 km/s?
答案 B
解析 设地球质量、半径分别为m、R,月球质量、半径分别为m、r,则m=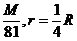 .在星体表面,物体的重力近似等于万有引力,若物体质量为m0,则
.在星体表面,物体的重力近似等于万有引力,若物体质量为m0,则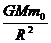 =m0g,即GM=gR2;在月球表面,满足:Gm=g′r2,由此可得:g′=
=m0g,即GM=gR2;在月球表面,满足:Gm=g′r2,由此可得:g′=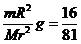 g,地球表面的第一宇宙速度v1=
g,地球表面的第一宇宙速度v1=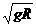 =7.9 km/s,在月球表面,有v′=
=7.9 km/s,在月球表面,有v′= ×7.9 km/s≈1.8 km/s.
×7.9 km/s≈1.8 km/s.
3.(06全国卷Ⅰ16)我国将要发射一颗绕月运行的探月卫星“嫦娥1号”.设该卫星的轨道是圆形的,且贴近月球表面.已知月球的质量约为地球质量的1/81,月球的半径约为地球半径的1/4,地球上的第一宇宙速度约为
2.(06重庆理综15)宇航员在月球上做自由落体实验,将某物体由距月球表面高h处释放,经时间t后落到月球表面(设月球半径为R).据上述信息推断,飞船在月球表面附近绕月球做匀速圆周运动所必须具有的速率为 ( )
A. 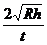 B.
B.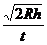 C.
C.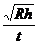 D.
D.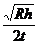
答案 B
解析 设月球表面的重力加速度为g月,绕月球表面做匀速圆周运动的线速度为v,根据万有引力定律:
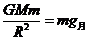 ①
①
绕月卫星: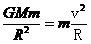 ②
②
根据月球表面物体做自由落体运动:
h =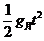 ③
③
由①②③得:v =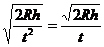
1.(06北京理综18)一飞船在某行星表面附近沿圆轨道绕该行星飞行,认为行星是密度均匀的球体,要确定该行星的密度,只需要测量 ( )
A.飞船的轨道半径 B.飞船的运行速度
C.飞船的运行周期 D.行星的质量
答案 C
解析 万有引力提供向心力,则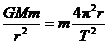 ,
,
由于飞船在行星表面附近飞行,其运行轨道半径r近似为行星的半径,所以满足M=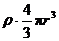 ,
,
联立得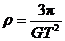 .
.
15.(06广东17)宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行.设每个星体的质量均为m.
(1)试求第一种形式下,星体运动的线速度和周期.
(2)假设两种形式下星体的运动周期相同,第二种形式下星体之间的距离应为多少?
答案
(1)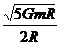
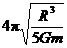 (2)
(2)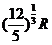
解析 (1)对于第一种运动情况,以某个运动星体为研究对象,根据牛顿第二定律和万有引力定律有:
F1=
F1+F2=mv2/R
运动星体的线速度:v =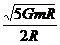
周期为T,则有T=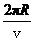
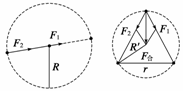 T=4π
T=4π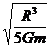
(2)设第二种形式星体之间的距离为r,则三个星体做圆周运动的半径为
R′=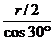
由于星体做圆周运动所需要的向心力靠其它两个星体的万有引力的合力提供,由力的合成和牛顿运动定律有:
F合=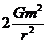 cos30°
cos30°
F合=m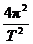 R′
R′
所以r=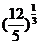 R
R
题组二
14.(06四川理综23)荡秋千是大家喜爱的一项体育活动.随着科技的迅速发展,将来的某一天,同学们也许会在其他星球上享受荡秋千的乐趣.假设你当时所在星球的质量是M、半径为R,可将人视为质点,秋千质量不计、摆长不变、摆角小于90°,万有引力常量为G.那么,
(1)该星球表面附近的重力加速度g星等于多少?
(2)若经过最低位置的速度为v0,你能上升的最大高度是多少?
答案 (1)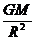 (2)
(2)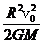
解析 (1)设人的质量为m,在星球表面附近的重力等于万有引力,有
mg星=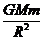
解得g星=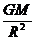
(2)设人能上升的最大高度为h,由功能关系得
mg星h=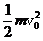
解得h=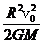
13.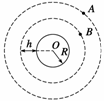 (06江苏14)如图所示,A是地球的同步卫星,另一卫星B的圆形轨道位于赤道平面
(06江苏14)如图所示,A是地球的同步卫星,另一卫星B的圆形轨道位于赤道平面
内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速
度为g,O为地球中心.
(1)求卫星B的运行周期.
(2)如卫星B绕行方向与地球自转方向相同,某时刻A、B两卫星相距最近(O、B、A在同一直线上),则至少经过多长时间,它们再一次相距最近?
答案 (1)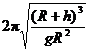 (2)
(2)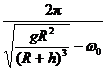
解析 (1)由万有引力定律和向心力公式得
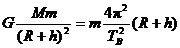 ①
①
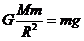 ②
②
联立①②得
TB=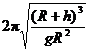 ③
③
(2)由题意得(ωB-ω0)t =2π ④
由③得ωB=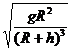 ⑤
⑤
代入④得t =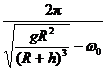
12.(07上海19A)宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处.(取地球表面重力加速度g=10 m/s2,空气阻力不计)
(1)求该星球表面附近的重力加速度g′.
(2)已知该星球的半径与地球半径之比为R星∶R地=1∶4,求该星球的质量与地球质量之比M星∶M地.
答案 (1)2 m/s2 (2)1∶80
解析 (1)在地球表面竖直上抛小球时,有t = ,在某星球表面竖直上抛小球时,有5t =
,在某星球表面竖直上抛小球时,有5t =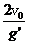
所以g′=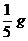 =2
m/s2
=2
m/s2
(2)由G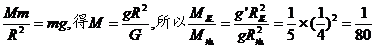
0.38 N.已知地球半径为6.4×103 km,请估算土星质量是地球质量的多少倍?
答案 (1)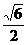 (2)
(2)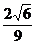 (3)95
(3)95
解析 (1)设土星质量为M0,颗粒质量为m,颗粒距土星中心距离为r,线速度为v,根据牛顿第二定律和万有引力定律得

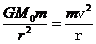 ①
①
解得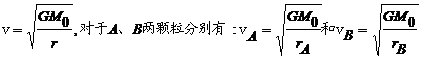
得: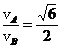 ②
②
(2)设颗粒绕土星做圆周运动的周期为T,则
 ③
③
对于A、B两颗粒分别有: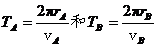
得: 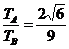 ④
④
(3)设地球质量为M,地球半径为r0,地球上物体的重力可视为万有引力,探测器上物体质量为m0,在地球表面重力为G0,距土星中心r0′=3.2×105 km处的引力为G0′,根据万有引力定律:
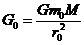 ⑤
⑤
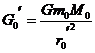 ⑥
⑥
由⑤⑥得: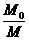 =95(倍)
=95(倍)
11.(07广东16)土星周围有许多大小不等的岩石颗粒,其绕土星的运动可视为圆周运动.其中有两个岩石颗粒A和B与土星中心的距离分别为rA=8.0×104 km和rB=1.2×105 km?,忽略所有岩石颗粒间的相互作用.(结果可用根式表示),求:
(1)岩石颗粒A和B的线速度之比.
(2)岩石颗粒A和B的周期之比.
(3)土星探测器上有一物体,在地球上重为10 N,推算出它在距土星中心3.2×105 km处受到土星的引力为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com