
4.归纳小结:对数的定义
 >0且
>0且 ≠1)
≠1)
 1的对数是零,负数和零没有对数
1的对数是零,负数和零没有对数
对数的性质 
 >0且
>0且 ≠1
≠1
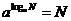
作业:P86 习题 2.2 A组 1、2
P88 B组 1
对数(第二课时)
3.计算 的值.
的值.
2.求 且不等于1,N>0).
且不等于1,N>0).
4、两类对数
① 以10为底的对数称为常用对数, 常记为
常记为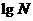 .
.
② 以无理数e=2.71828…为底的对数称为自然对数,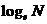 常记为
常记为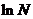 .
.
以后解题时,在没有指出对数的底的情况下,都是指常用对数,如100的对数等于2,即 .
.
说明:在例1中,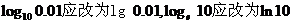 .
.
例2:求下列各式中x的值
(1)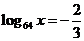 (2)
(2)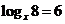 (3)
(3)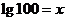 (4)
(4)
分析:将对数式化为指数式,再利用指数幂的运算性质求出x.
解:(1)
(2)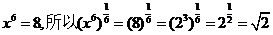
(3)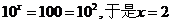
(4)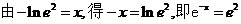
所以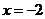
课堂练习:P74 练习3、4
补充练习:1. 将下列指数式与对数式互化,有 的求出
的求出 的值 .
的值 .
(1) (2)
(2) (3)
(3)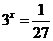
(4) (5)
(5)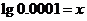 (6)
(6)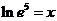
3.对数的性质:
提问:因为 >0,
>0, ≠1时,
≠1时,
则 由1、 0=1 2、
0=1 2、 1=
1= 如何转化为对数式
如何转化为对数式
②负数和零有没有对数?
③根据对数的定义,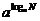 =?
=?
(以上三题由学生先独立思考,再个别提问解答)
由以上的问题得到
①  (
( >0,且
>0,且 ≠1)
≠1)
② ∵ >0,且
>0,且 ≠1对任意的力,
≠1对任意的力, 常记为
常记为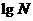 .
.
恒等式: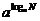 =N
=N
2、对数式与指数式的互化
在对数的概念中,要注意:
(1)底数的限制 >0,且
>0,且 ≠1
≠1
(2)
指数式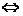 对数式
对数式
幂底数← →对数底数
→对数底数
指 数← →对数
→对数
幂 ←N→真数
说明:对数式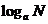 可看作一记号,表示底为
可看作一记号,表示底为 (
( >0,且
>0,且 ≠1),幂为N的指数工表示方程
≠1),幂为N的指数工表示方程 (
( >0,且
>0,且 ≠1)的解. 也可以看作一种运算,即已知底为
≠1)的解. 也可以看作一种运算,即已知底为 (
( >0,且
>0,且 ≠1)幂为N,求幂指数的运算. 因此,对数式
≠1)幂为N,求幂指数的运算. 因此,对数式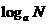 又可看幂运算的逆运算.
又可看幂运算的逆运算.
例题:
例1(P73例1)
将下列指数式化为对数式,对数式化为指数式.
(1)54=645
(2) (3)
(3)
(4)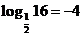 (5)
(5)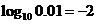 (6)
(6)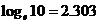
注:(5)、(6)写法不规范,等到讲到常用对数和自然对数后,再向学生说明.
(让学生自己完成,教师巡视指导)
巩固练习:P74 练习 1、2
1、对数的概念
一般地,若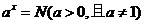 ,那么数
,那么数 叫做以a为底N的对数,记作
叫做以a为底N的对数,记作
 叫做对数的底数,N叫做真数.
叫做对数的底数,N叫做真数.
举例:如: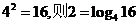 ,读作2是以4为底,16的对数.
,读作2是以4为底,16的对数.
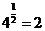 ,则
,则 ,读作
,读作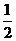 是以4为底2的对数.
是以4为底2的对数.
提问:你们还能找到那些对数的例子
1.提出问题
思考:(P72思考题)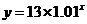 中,哪一年的人口数要达到10亿、20亿、30亿……,该如何解决?
中,哪一年的人口数要达到10亿、20亿、30亿……,该如何解决?
即: 在个式子中,
在个式子中, 分别等于多少?
分别等于多少?
象上面的式子,已知底数和幂的值,求指数,这就是我们这节课所要学习的对数(引出对数的概念).
(1)学法:讲授法、讨论法、类比分析与发现
(2)教具:投影仪
(1)重点:对数式与指数式的互化及对数的性质
(2)难点:推导对数性质的
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com