
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
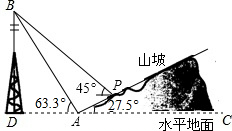 如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)
如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)查看答案和解析>>
科目:初中数学 来源: 题型:
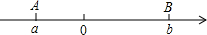 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.查看答案和解析>>
科目:初中数学 来源: 题型:
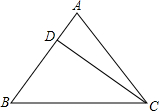 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,
已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com