
分析 ①△ABC是锐角三角形时,先根据高线的定义求出∠ADB=90°,∠BEC=90°,然后根据直角三角形两锐角互余求出∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解;
②△ABC是钝角三角形时,根据直角三角形两锐角互余求出∠BHC=∠A,从而得解.
解答 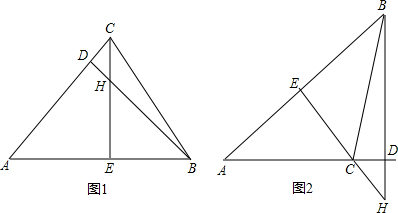 解:①如图1,△ABC是锐角三角形时,
解:①如图1,△ABC是锐角三角形时,
∵BD、CE是△ABC的高线,
∴∠ADB=90°,∠BEC=90°,
在△ABD中,∵∠A=45°,
∴∠ABD=90°-45°=45°,
∴∠BHC=∠ABD+∠BEC=45°+90°=135°;
②如图2,△ABC是钝角三角形时,
∵BD、CE是△ABC的高线,
∴∠A+∠ACE=90°,∠BHC+∠HCD=90°,
∵∠ACE=∠HCD(对顶角相等),
∴∠BHC=∠A=45°.
综上所述,∠BHC的度数是135°或45°.
点评 本题主要考查了三角形的内角和定理,三角形的高线,难点在于要分△ABC是锐角三角形与钝角三角形两种情况讨论,作出图形更形象直观.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+6)(a-6)=a2-12 | B. | (x+5)(x-6)=x2-30 | ||
| C. | (a+1)2=a2+1 | D. | (-5xy-2)(2-5xy)=25x2y2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
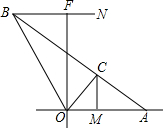 如图,一轮渡从B点出发沿东偏南25°方向匀速航行,经过4.5分钟后达到C处,若保持航线不变,继续航行可直接到达停靠码头A,在停靠码头A的正西反向500m处有一观察站O,在O处测得B位于其北偏西35°,C位于其北偏东55°.求C处到海岸线OA的距离大约是多少米?
如图,一轮渡从B点出发沿东偏南25°方向匀速航行,经过4.5分钟后达到C处,若保持航线不变,继续航行可直接到达停靠码头A,在停靠码头A的正西反向500m处有一观察站O,在O处测得B位于其北偏西35°,C位于其北偏东55°.求C处到海岸线OA的距离大约是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,0) | B. | (2.5,0) | C. | (3,0) | D. | (4,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
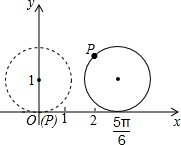 如图,在平面直角坐标系中,半径为1的圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动,当滚动到圆心位于($\frac{5π}{6}$,1)时,点P的坐标是($\frac{5π-3}{6}$,$\frac{2+\sqrt{3}}{2}$).
如图,在平面直角坐标系中,半径为1的圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动,当滚动到圆心位于($\frac{5π}{6}$,1)时,点P的坐标是($\frac{5π-3}{6}$,$\frac{2+\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知实数a、b、c在数轴上的位置如图所示,试化简:$\sqrt{{{(-c)}^2}}-|{a-c}|+\sqrt{{{(a+b)}^2}}-|{b+c}|$.
已知实数a、b、c在数轴上的位置如图所示,试化简:$\sqrt{{{(-c)}^2}}-|{a-c}|+\sqrt{{{(a+b)}^2}}-|{b+c}|$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,O为△ABC的外心,△OCP为正三角形,OP与AC相交于D点,连接OA.若∠BAC=69°14′,AB=AC,则∠ADP的度数85°23′.
如图,O为△ABC的外心,△OCP为正三角形,OP与AC相交于D点,连接OA.若∠BAC=69°14′,AB=AC,则∠ADP的度数85°23′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com