
分析 (1)①利用绝对值的性质去绝对值,进而比较大小;
②利用绝对值的性质去绝对值,进而比较大小;
③利用绝对值的性质去绝对值,进而比较大小;
④利用绝对值的性质去绝对值,进而比较大小;
(2)根据绝对值的性质结合,当a,b异号时,当a,b同号时分析得出答案;
(3)利用(2)中结论进而分析得出答案.
解答 解:(1)①∵|-2|+|3|=5,|-2+3|=1,
∴|-2|+|3|>|-2+3|;
②∵$|{-\frac{1}{2}}|$+$|{-\frac{1}{3}}|$=$\frac{5}{6}$,$|{-\frac{1}{2}-\frac{1}{3}}|$=$\frac{5}{6}$,
∴$|{-\frac{1}{2}}|$+$|{-\frac{1}{3}}|$=$|{-\frac{1}{2}-\frac{1}{3}}|$;
③∵|6|+|-3|=9,|6-3|=3,
∴|6|+|-3|>|6-3|;
④∵|0|+|-8|=8,|0-8|=8,
∴|0|+|-8|=|0-8|;
(2)当a,b异号时,|a|+|b|>|a+b|,
当a,b同号时,|a|+|b|=|a+b|,
∴|a|+|b|≥|a+b|;
(3)由(2)中得出的结论可知,x与-2015同号,
当|x|+2015=|x-2015|时,则x的取值范围是:x≤0.
当|a1+a2|+|a3+a4|=15,|a1+a2+a3+a4|=5,
可得a1+a2和a3+a4异号,
则a1+a2=10或-10或5或-5.
故答案为:x≤0;10或-10或5或-5.
点评 此题主要考查了绝对值,根据题意得出a,b直接符号的关系是解题关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
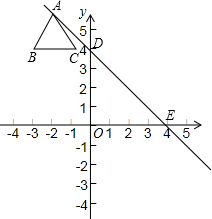 在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.
在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com