
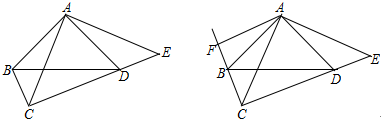
分析 (1)先求出∴∠ABC=∠ADE,再根据三角形的判定定理ASA即可证得.
(2)过点A作AM⊥CE,垂足为M;通过三角形全等求得AC=AE,∠BCA=∠E,进而根据等边对等角求得∠ACD=∠E,从而求得∠BCA=∠ACD,再根据角的平分线的性质求得AF=AM,然后证得△CAE和△ACM是等腰直角三角形,进而得出EC=2AF.
解答 (1)证明:∵∠BAD=∠BCD=90°,
∴∠ABC+∠ADC=180°,
又∵∠ADE+∠ADC=180°,
∴∠ABC=∠ADE,
在△ABC与△ADE中,$\left\{\begin{array}{l}{∠BAC=∠DAE}&{\;}\\{AB=AD}&{\;}\\{∠ABC=∠ADE}&{\;}\end{array}\right.$,
∴△ABC≌△ADE(ASA);
(2)证明:过点A作AM⊥CE,垂足为M,如图所示: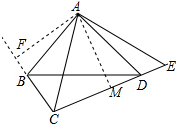
∵△ABC≌△ADE,
∴AC=AE,∠BCA=∠E,
∴∠ACD=∠E,
∴∠BCA=∠ACD,
∵AM⊥CD,AF⊥CF,
∴AF=AM,
又∵∠BAC=∠DAE,
∴∠CAE=∠CAD+∠DAE=∠CAD+∠BAC=∠BAD=90°,
∵AC=AE,∠CAE=90°,
∴∠ACE=∠AEC=45°,
∵AM⊥CE,
∴∠ACE=∠CAM=∠MAE=∠E=45°,
∴CM=AM=ME,
又∵AF=AM,
∴EC=2AF.
点评 此题考查了全等三角形的判定与性质、角的平分线的判定和性质以及等腰三角形的判定与性质;熟练掌握全等三角形的判定与性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
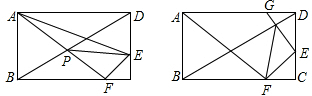
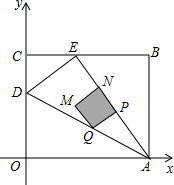 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.线段AE上有一动点P(不与A重合),从A点开始沿AE方向匀速运动,到达点E时停止.运动的速度为每秒2个单位长度,设运动的时间为t秒,过P点作AE的垂线交AD于点Q,以PQ为边向上作正方形PQMN,正方形PQMN与矩形ABCO重叠部分(阴影部分)面积为S(平方单位).
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.线段AE上有一动点P(不与A重合),从A点开始沿AE方向匀速运动,到达点E时停止.运动的速度为每秒2个单位长度,设运动的时间为t秒,过P点作AE的垂线交AD于点Q,以PQ为边向上作正方形PQMN,正方形PQMN与矩形ABCO重叠部分(阴影部分)面积为S(平方单位).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
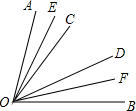 如图,∠COD在∠AOB的内部绕点O进行旋转,∠AOD+∠BOC=110°,∠AOC+∠BOD=50°,OE,OF分别是∠AOC与∠BOD的平分线.
如图,∠COD在∠AOB的内部绕点O进行旋转,∠AOD+∠BOC=110°,∠AOC+∠BOD=50°,OE,OF分别是∠AOC与∠BOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com