
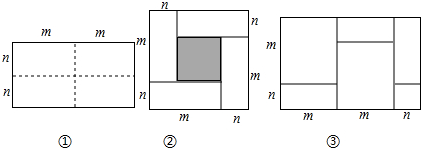
分析 (1)①观察可得阴影部分的正方形边长是m-n;
②方法1:阴影部分的面积就等于边长为m-n的小正方形的面积;方法2:边长为m+n的大正方形的面积减去4个长为m,宽为n的长方形面积;
③根据以上相同图形的面积相等可得;
(2)根据|m+n-6|+|mn-4|=0可得m+n=6、mn=4,利用(1)中结论(m-n)2=(m+n)2-4mn计算可得;
(3)根据:大长方形面积等于长乘以宽或两个边长分别为m、n的正方形加上3个长为m、宽为n的小长方形面积和列式可得.
解答 解:(1)①阴影部分的正方形边长是m-n.
②方法1:阴影部分的面积就等于边长为m-n的小正方形的面积,即(m-n)2,
方法2:边长为m+n的大正方形的面积减去4个长为m,宽为n的长方形面积,即(m+n)2-4mn;
③(m-n)2=(m+n)2-4mn.
(2))∵|m+n-6|+|mn-4|=0,
∴m+n-6=0,mn-4=0,
∴m+n=6,mn=4
∵由(1)可得(m-n)2=(m+n)2-4mn
∴(m-n)2=(m+n)2-4mn=62-4×4=20,
∴(m-n)2=20;
(3)根据大长方形面积等于长乘以宽有:(2m+n)(m+n),
或两个边长分别为m、n的正方形加上3个长为m、宽为n的小长方形面积和有:2m2+3mn+n2,
故可得:(2m+n)(m+n)=2m2+3mn+n2.
故答案为:(1)m-n;(2)①(m-n)2,②(m+n)2-4mn,③(m-n)2=(m+n)2-4mn;(3)(2m+n)(m+n)=2m2+3mn+n2.
点评 本题考查了完全平方公式的几何意义,认真观察图形以及掌握正方形、长方形的面积公式计算是关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com