
 解:由题意可知,当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.
解:由题意可知,当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.
|
|


科目:初中数学 来源: 题型:
| 购买香蕉数 (千克) | 不超过20千克 | 20千克以上但不超过40千克 | 40千克以上 |
| 每千克价格(元) | 6元 | 5元 | 4元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x+1 |
| x |
| x2-1 |
| 1 |
| x |
| 1 |
| y |
| 2x+3xy+2y |
| 3x-2xy+3y |
查看答案和解析>>
科目:初中数学 来源: 题型:
| m |
| x |
| k |
| x |
| m |
| x |
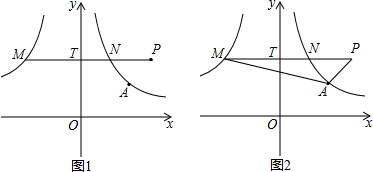
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
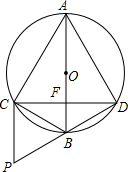 若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=
若AC=AD,∠CAD=60°,AB与CD相交于点F,AF=| 8 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
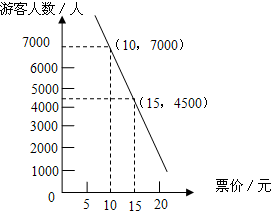 某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?
某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
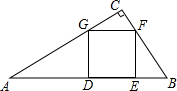 如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.
如图,在Rt△ABC中,∠C=90°,正方形DEFG的顶点D,E在AB边上,F,G分别在BC和AC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com