
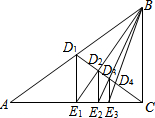
 如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.若S△ABC=1,则S2010=$\frac{1}{201{1}^{2}}$.
如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.若S△ABC=1,则S2010=$\frac{1}{201{1}^{2}}$. 分析 根据直角三角形的性质以及相似三角形的性质.再利用在△ACB中,D2为其重心可得D2E1=$\frac{1}{3}$BE1,然后从中找出规律即可解答.
解答 解:易知D1E1∥BC,∴△BD1E1与△CD1E1同底同高,面积相等,以此类推;
根据直角三角形的性质以及相似三角形的性质可知:D1E1=$\frac{1}{2}$BC,CE1=$\frac{1}{2}$AC,S1=$\frac{1}{{2}^{2}}$S△ABC;
∴在△ACB中,D2为其重心,
∴D2E1=$\frac{1}{3}$BE1,
∴D2E2=$\frac{1}{3}$BC,CE2=$\frac{1}{3}$AC,S2=$\frac{1}{{3}^{2}}$S△ABC,
∵D2E2:D1E1=2:3,D1E1:BC=1:2,
∴BC:D2E2=2D1E1:$\frac{2}{3}$D1E1=3,
∴CD3:CD2=D3E3:D2E2=CE3:CE2=3:4,
∴D3E3=$\frac{3}{4}$D2E2=$\frac{3}{4}$×$\frac{1}{3}$BC=$\frac{1}{4}$BC,CE3=$\frac{3}{4}$CE2=$\frac{3}{4}$×$\frac{1}{3}$AC=$\frac{1}{4}$AC,S3=$\frac{1}{{4}^{2}}$S△ABC…;
∴Sn=$\frac{1}{(n+1)^{2}}$S△ABC,
∵S△ABC=1,
∴S2010=$\frac{1}{201{1}^{2}}$.
故答案为:$\frac{1}{201{1}^{2}}$.
点评 本题考查了相似三角形的判定与性质,解决本题的关键是据直角三角形的性质以及相似三角形的性质得到第一个三角形的面积与原三角形的面积的规律.也考查了重心的性质即三角形三边中线的交点到顶点的距离等于它到对边中点距离的两倍.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.
学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
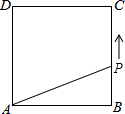 如图,在边长为$\sqrt{2}$的正方形ABCD的一边BC上,有一点P从B点运动到C点,设PB=x,四边形APCD的面积为y.写出y与x之间的关系式为y=-$\frac{\sqrt{2}}{2}$x+2(0≤x<$\sqrt{2}$)(要写出自变量的取值范围).
如图,在边长为$\sqrt{2}$的正方形ABCD的一边BC上,有一点P从B点运动到C点,设PB=x,四边形APCD的面积为y.写出y与x之间的关系式为y=-$\frac{\sqrt{2}}{2}$x+2(0≤x<$\sqrt{2}$)(要写出自变量的取值范围).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com