
【题目】为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,己知成绩x(单位:分)均满足“50≤x<100”,每组成绩包含最小值,不包含最大值.根据图中信息回答下列问题:
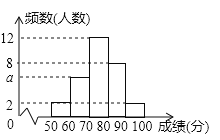
(1)图中a的值为_____;若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为__________;
(2)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有多少人?
(3)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.
【答案】(1)6,144°;(2)100人;(3)见解析,![]() .
.
【解析】
(1)用总人数减去其他分组的人数即可求得60![]() x<70的人数a;用360乘以成绩在70≤x<80的人数所占比例可得;
x<70的人数a;用360乘以成绩在70≤x<80的人数所占比例可得;
(2)用总人数乘以样本中优秀人数所占比例即可得;
(3)先画出树状图展示所有12种等可能的结果数,再找出有C的结果数,然后根据概率公式求解.
解:(1)a=30-(2+12+8+2)=6;成绩在“70≤x<80所对应扇形的圆心角度数为360°×![]() =144°;故答案为:6,144;
=144°;故答案为:6,144;
(2)获得“优秀“的学生大约有300×![]() =100人,故答案为:100人;
=100人,故答案为:100人;
(3)50≤x<60的两名同学用A、B表示,90≤x<100的两名同学用C(小明)、D表示,画树状图如下:

由树状图知共有12种等可能结果,其中小明被选中的结果数为6,
∴小明被选中的概率为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】自习课上小明在准备完成题目:化简:( ![]() x2+6x+8)-(6x+8x2+2)发现系数“
x2+6x+8)-(6x+8x2+2)发现系数“ ![]() ” 印刷不清楚、
” 印刷不清楚、
(1)他把“ ![]() ”猜成6,请你帮小明完成化简:(6x2+6x+8)-(6x+8x2+2);
”猜成6,请你帮小明完成化简:(6x2+6x+8)-(6x+8x2+2);
(2)小明同桌看到他化简的结果说:“你猜错了,我看到该题标准答案的结果是常数。”请你通过计算说明原题中“ ![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知Rt△ABC中,∠ACB=90°,AC=8,AB=10,点D是AC边上一点(不与C重合),以AD为直径作⊙O,过C作CE切⊙O于E,交AB于F.
(1)若⊙O半径为2,求线段CE的长;
(2)若AF=BF,求⊙O的半径;
(3)如图②,若CE=CB,点B关于AC的对称点为点G,试求G、E两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
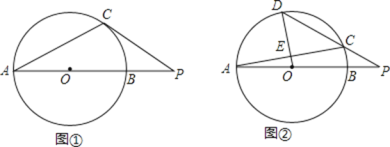
【题目】在![]() 中, AB为直径, C 为
中, AB为直径, C 为![]() 上一点。
上一点。
(1)如图 1. 过点 C 作 O 的切线 , 与 AB 的延长线相交于点 P, 若 ∠CAB=27°,求 ∠P 的大小;
(2)如图 2,D 为![]() 上一点 , 且 OD 经过 AC 的中点 E, 连接 DC 并延长 , 与 AB 的延长线相交于点 P, 若 ∠CAB=10°,求 ∠P 的大小.
上一点 , 且 OD 经过 AC 的中点 E, 连接 DC 并延长 , 与 AB 的延长线相交于点 P, 若 ∠CAB=10°,求 ∠P 的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有![]() 棵橘子树,平均每一棵树结
棵橘子树,平均每一棵树结![]() 个橘子.根据经验估计,每多种
个橘子.根据经验估计,每多种![]() 棵树,平均每棵树就会少结
棵树,平均每棵树就会少结![]() 个橘子.设果园增种
个橘子.设果园增种![]() 棵橘子树,果园橘子总个数为
棵橘子树,果园橘子总个数为![]() 个.
个.
(1)根据题意,填写下表:
增种的橘子树(棵) |
|
|
|
| … |
|
平均每棵树结橘子数(个) |
|
(2)求果园里增种多少棵橘子树时,所结橘子总数最多,并求出此时橘子的总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过原点,与x轴交于另一点A,对称轴x=-2交x轴于点C,直线l过点N(0,-2),且与x轴平行,过点P作PM⊥l于点M,△AOB的面积为2.
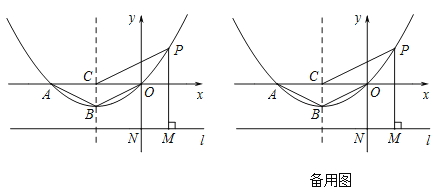
(1)求抛物线的解析式;
(2)当∠MPN=∠BAC时,求P点坐标;
(3)①求证PM=PC;
②若点Q坐标为(0,2),直接写出PQ+PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.
与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 公司
公司![]() 年使用自主研发生产的“
年使用自主研发生产的“![]() ”系列甲、乙、丙三类芯片共
”系列甲、乙、丙三类芯片共![]() 万块,生产了
万块,生产了![]() 万部手机,其中乙类芯片的产量是甲类芯片的
万部手机,其中乙类芯片的产量是甲类芯片的![]() 倍,丙类芯片的产量比甲、乙两类芯片产量的和还多
倍,丙类芯片的产量比甲、乙两类芯片产量的和还多![]() 万块.这些“
万块.这些“![]() ”芯片解决了该公司
”芯片解决了该公司![]() 年生产的全部手机所需芯片的
年生产的全部手机所需芯片的![]() .
.
(1)求![]() 年甲类芯片的产量;
年甲类芯片的产量;
(2)![]() 公司计划
公司计划![]() 年生产的手机全部使用自主研发的“
年生产的手机全部使用自主研发的“![]() ”系列芯片.从
”系列芯片.从![]() 年起逐年扩大“
年起逐年扩大“![]() ”芯片的产量,
”芯片的产量,![]() 年、
年、![]() 年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数
年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数![]() ,乙类芯片的产量平均每年增长的百分数比
,乙类芯片的产量平均每年增长的百分数比![]() 小
小![]() ,丙类芯片的产量每年按相同的数量递增.
,丙类芯片的产量每年按相同的数量递增.![]() 年到
年到![]() 年,丙类芯片三年的总产量达到
年,丙类芯片三年的总产量达到![]() 亿块.这样,
亿块.这样,![]() 年的
年的![]() 公司的手机产量比
公司的手机产量比![]() 年全年的手机产量多
年全年的手机产量多![]() ,求丙类芯片
,求丙类芯片![]() 年的产量及
年的产量及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
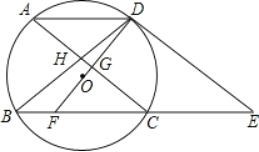
【题目】如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5cm,AC=8cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com