
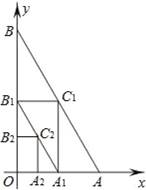
如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB=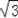
 ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 .

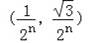
 .
.
【考点】规律型:点的坐标.
【专题】规律型.
【分析】首先利用三角形中位线定理可求出B1C1的长和C1A1的长,即C1的横坐标和纵坐标,以此类推即可求出点Cn的坐标.
【解答】解:∵过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,
∴B1C1和C1A1是三角形OAB的中位线,
∴B1C1=
 OA=
OA=
 ,C1A1=
,C1A1=
 OB=
OB=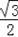
 ,
,
∴C1的坐标为(
 ,
,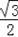
 ),
),
同理可求出B2C2=
 =
=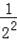
 ,C2A2=
,C2A2=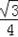
 =
=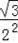

∴C2的坐标为(
 ,
,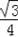
 ),
),
…以此类推,
可求出BnCn=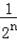
 ,CnAn=
,CnAn=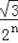
 ,
,
∴点Cn的坐标为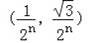
 ,
,
故答案为: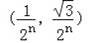
 .
.
【点评】本题考查了规律型:点的坐标的求解,用到的知识点是三角形中位线定理,解题的关键是正确求出C1和C2点的坐标,由此得到问题的一般规律.


科目:初中数学 来源: 题型:
某生态农业园种植的青椒除了运往市区销售外,还可以让市民亲自去生态农业园购买.已知今年5月份该青椒在市区、园区的销售价格分别为6元/千克、4元/千克,今年5月份一共销售了3000千克,总销售额为16000元.
(1)今年5月份该青椒在市区、园区各销售了多少千克?
(2)6月份是青椒产出旺季.为了促销,生态农业园决定6月份将该青椒在市区、园区的销售价格均在今年5月份的基础上降低a%,预计这种青椒在市区、园区的销售量将在今年5月份的基础上分别增长30%、20%,要使6月份该青椒的总销售额不低于18360元,则a的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
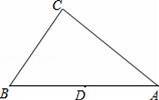
如图,△ABC中,AB=5,BC=3,CA=4,D为AB的中点,过点D的直线与BC交于点E,若直线DE截△ABC所得的三角形与△ABC相似,则DE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
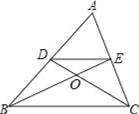
如图,在△ABC中两条中线BE、CD相交于点O,记△DOE的面积为S1,△COB的面积为S2,则S1:S2=( )

A.1:4 B.2:3 C.1:3 D.1:2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com