
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() ÷·µƒ’˝∞Î÷·…œ£¨Ω´œþ∂Œ
÷·µƒ’˝∞Î÷·…œ£¨Ω´œþ∂Œ![]() »∆µ„
»∆µ„![]() À≥ ±’Ζ˝◊™90°„µ√µΩ
À≥ ±’Ζ˝◊™90°„µ√µΩ![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() ÷·µƒ¥πœþ£¨¥π◊„Œ™
÷·µƒ¥πœþ£¨¥π◊„Œ™![]() £¨¡¨Ω”
£¨¡¨Ω”![]() Ωª
Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £Æ
£Æ
£®1£©µ±µ„![]() ‘⁄µ⁄»˝œÛœÞ ±£¨«Û µ ˝
‘⁄µ⁄»˝œÛœÞ ±£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨…Ë![]() £¨µ±
£¨µ±![]() »°µ√◊Ó¥Û÷µ ±£¨«ÛÕºœÛæ≠π˝
»°µ√◊Ó¥Û÷µ ±£¨«ÛÕºœÛæ≠π˝![]() ¡Ωµ„µƒ∂˛¥Œ∫Ø ˝
¡Ωµ„µƒ∂˛¥Œ∫Ø ˝![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨Ω´÷±œþ![]() œÚ…œ∆Ω“∆
œÚ…œ∆Ω“∆![]() ∏ˆµ•Œª∫Û”Î∂˛¥Œ∫Ø ˝
∏ˆµ•Œª∫Û”Î∂˛¥Œ∫Ø ˝![]() µƒÕºœÛΩªµ„µƒ∫·◊¯±ÍŒ™
µƒÕºœÛΩªµ„µƒ∫·◊¯±ÍŒ™![]() £¨»Ù
£¨»Ù![]() £¨«Û
£¨«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©
£ª£®2£©![]() £ª£®3£©
£ª£®3£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
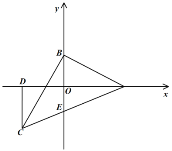
£®1£©Ω´µ„BœÚœ¬∆Ω“∆m∏ˆµ•Œª£¨¥À ±µ„A°‰£®6£¨©Åm£©£¨Ω´¥À ±µ„AB»∆µ„BÀ≥ ±’Ζ˝◊™90°„µ√µΩµ„C°‰£®©Åm£¨©Å6£©£¨Ω´µ„C°‰œÚ…œ∆Ω“∆mµƒµ•Œªµ√µΩµ„C£®©Åm£¨m©Å6£©£¨º¥ø…«ÛΩ‚£ª
£®2£©S£ΩS°˜ABO+S°˜ADC£Ω![]() °¡AO°¡BO+
°¡AO°¡BO+![]() °¡AD°¡CD£Ω
°¡AD°¡CD£Ω![]() °¡6°¡m+
°¡6°¡m+![]() °¡£®6+m£©°¡£®6©Åm£©£Ω©Å
°¡£®6+m£©°¡£®6©Åm£©£Ω©Å![]() m2+3m+18£¨π S”–◊Ó¥Û÷µ£¨¥À ±£¨m£Ω3£¨º¥ø…«ÛΩ‚£ª
m2+3m+18£¨π S”–◊Ó¥Û÷µ£¨¥À ±£¨m£Ω3£¨º¥ø…«ÛΩ‚£ª
£®3£©∫Ø ˝µƒΩªµ„µƒ∫·◊¯±ÍŒ™x0£¨»Ùx0°ð©Å3£¨‘Úx£Ω©Å3 ±£¨≈◊ŒÔœþ‘⁄÷±œþµƒ…œ∑Ω£¨º¥ø…«ÛΩ‚£Æ
Ω‚£∫£®1£©Ω´µ„BœÚœ¬∆Ω“∆m∏ˆµ•Œª£¨¥À ±µ„A°‰£®6£¨©Åm£©£¨Ω´¥À ±µ„AB»∆µ„BÀ≥ ±’Ζ˝◊™90°„µ√µΩµ„C°‰£®©Åm£¨©Å6£©£¨
Ω´µ„C°‰œÚ…œ∆Ω“∆mµƒµ•Œªµ√µΩµ„C£®©Åm£¨m©Å6£©£¨
µ„C‘⁄µ⁄»˝œÛœÞ ±£¨©Åm£º0«“m©Å6£º0£¨
Ω‚µ√£∫0£ºm£º6£ª
£®2£©S£ΩS°˜ABO+S°˜ADC£Ω![]() °¡AO°¡BO+
°¡AO°¡BO+![]() °¡AD°¡CD£Ω
°¡AD°¡CD£Ω![]() °¡6°¡m+
°¡6°¡m+![]() °¡£®6+m£©°¡£®6©Åm£©£Ω©Å
°¡£®6+m£©°¡£®6©Åm£©£Ω©Å![]() m2+3m+18£¨
m2+3m+18£¨
°þ©Å![]() £º0£¨π S”–◊Ó¥Û÷µ£¨¥À ±£¨m£Ω3£¨
£º0£¨π S”–◊Ó¥Û÷µ£¨¥À ±£¨m£Ω3£¨
𠵄C£®©Å3£¨©Å3£©£¨µ„A£®6£¨0£©£¨
Ω´µ„C°¢Aµƒ◊¯±Í¥˙»Î“ª¥Œ∫Ø ˝±Ì¥Ô Ω≤¢Ω‚µ√£∫
÷±œþACµƒ±Ì¥Ô ΩŒ™£∫y£Ω![]() x©Å2£¨π µ„E£®0£¨©Å2£©£¨
x©Å2£¨π µ„E£®0£¨©Å2£©£¨
‘Úc£Ω©Å2£¨Ω´µ„Aµƒ◊¯±Í¥˙»Î≈◊ŒÔœþ±Ì¥Ô Ωµ√£∫0£Ω36a©Å6©Å2£¨Ω‚µ√£∫a£Ω![]() £¨
£¨
π ≈◊ŒÔœþµƒ±Ì¥Ô ΩŒ™£∫y£Ω![]() x2©Åx©Å2°≠¢Ÿ£ª
x2©Åx©Å2°≠¢Ÿ£ª
£®3£©÷±œþy£Ω£®2©Åk£©x+2œÚ…œ∆Ω“∆k∏ˆµ•Œª∫Ûµ√µΩ∫Ø ˝Œ™£∫y£Ω£®2©Åk£©x+2+2°≠¢⁄£¨
¡™¡¢¢Ÿ¢⁄≤¢’˚¿Ìµ√£∫![]() x2©Å£®3©Åk£©x©Å4©Åk£Ω0£¨
x2©Å£®3©Åk£©x©Å4©Åk£Ω0£¨
°˜£Ω£®3©Åk£©2+![]() £®4+k£©£Ωk2©Å
£®4+k£©£Ωk2©Å![]() k+
k+![]() £æ0£¨
£æ0£¨
π ≈◊ŒÔœþ”⁄÷±œþ”–¡Ω∏ˆΩªµ„£¨
Ωªµ„µƒ∫·◊¯±ÍŒ™x0£¨»Ùx0°ð©Å3£¨‘Úx£Ω©Å3 ±£¨≈◊ŒÔœþ‘⁄÷±œþµƒ…œ∑Ω£¨
µ±x£Ω©Å3 ±£¨y£Ω![]() x2©Åx©Å2£Ω3£¨
x2©Åx©Å2£Ω3£¨
µ±x£Ω©Å3 ±£¨y£Ω£®2©Åk£©x+2+2£Ω4k©Å4£¨
º¥4k©Å4°Ð3£¨
Ω‚µ√£∫k°Ð![]() £Æ
£Æ


 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£ª˝º´ø™’π°∞—Ùπ‚Ô˝°±ªÓ∂Ø£¨≤¢ø™…Ë¡Àï…˛°¢◊„«Ú°¢¿∫«Ú°¢≈Ð≤ΩÀƒ÷÷‘À∂؜Ӄø£¨Œ™¡ÀΩ‚—ß…˙◊Óœ≤∞ƃƒ“ª÷÷œÓƒø£¨Àʪ˙≥È»°¡À≤ø∑÷—ß…˙Ω¯––µ˜≤È£¨≤¢ªÊ÷∆¡À»Áœ¬µƒÃı–ŒÕ≥º∆Õº∫Õ…»–ŒÕ≥º∆Õº£®≤ø∑÷–≈œ¢Œ¥∏¯≥ˆ£©£Æ
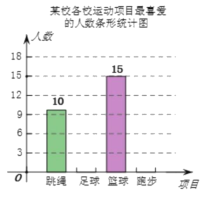
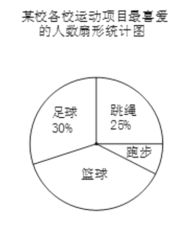
£®1£©«Û±æ¥Œ±ªµ˜≤ȵƒ—ß…˙»À ˝£ª
£®2£©≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©‘⁄…»–ŒÕ≥º∆Õº÷–£¨°∞¿∫«Ú°±≤ø∑÷À˘∂‘”¶µƒ‘≤–ƒΩ«∂» ˝Œ™__ £ª
£®4£©∏√–£π≤”–3000√˚—ß…˙£¨«Îπ¿º∆»´–£◊Óœ≤∞Æ¿∫«Úµƒ»À ˝±»◊Óœ≤∞Æ◊„«Úµƒ»À ˝∂ý∂ý…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
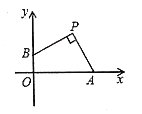
°æƒø°ø»ÁÕº£¨“—÷™AB «![]() µƒ÷±æ∂£¨µ„P‘⁄BAµƒ—”≥§œþ…œ£¨PD«–
µƒ÷±æ∂£¨µ„P‘⁄BAµƒ—”≥§œþ…œ£¨PD«–![]() ”⁄µ„D£¨π˝µ„B◊˜
”⁄µ„D£¨π˝µ„B◊˜![]() £¨ΩªPDµƒ—”≥§œþ”⁄µ„C£¨¡¨Ω”AD≤¢—”≥§£¨ΩªBE”⁄µ„E£Æ
£¨ΩªPDµƒ—”≥§œþ”⁄µ„C£¨¡¨Ω”AD≤¢—”≥§£¨ΩªBE”⁄µ„E£Æ
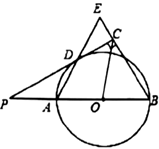
(¢Ò)«Û÷§£∫AB=BE£ª
(¢Ú)¡¨Ω·OC£¨»Áπ˚PD=2![]() £¨°œABC=60°„£¨«ÛOCµƒ≥§£Æ
£¨°œABC=60°„£¨«ÛOCµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() £¨
£¨![]() ∑÷±‘⁄
∑÷±‘⁄![]() ÷·£¨
÷·£¨![]() ÷·µƒ’˝∞Î÷·…œ‘À∂Ø£¨«“
÷·µƒ’˝∞Î÷·…œ‘À∂Ø£¨«“![]() £¨œ¬¡–Ω·¬€£∫
£¨œ¬¡–Ω·¬€£∫
¢Ÿ![]()
¢⁄µ±![]() ±Àƒ±þ–Œ
±Àƒ±þ–Œ![]() «’˝∑Ω–Œ
«’˝∑Ω–Œ
¢€Àƒ±þ–Œ![]() µƒ√ʪ˝∫Õ÷Ð≥§∂º «∂®÷µ
µƒ√ʪ˝∫Õ÷Ð≥§∂º «∂®÷µ
¢Ð¡¨Ω”![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() £¨∆‰÷–’˝»∑µƒ”–£® £©
£¨∆‰÷–’˝»∑µƒ”–£® £©
A.¢Ÿ¢⁄B.¢Ÿ¢⁄¢€C.¢Ÿ¢⁄¢ÐD.¢Ÿ¢⁄¢€¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£—ß…˙ª·∑¢œ÷Õ¨—ß√«æÕ≤Õ ± £”ý∑π≤ÀΩœ∂ý£¨¿À∑——œ÷ÿ£¨”⁄ «◊º±∏‘⁄–£ƒ⁄≥´µº°∞π‚≈Ö–∂Ø°±£¨»√Õ¨—ß√«’‰œß¡∏ ≥£¨Œ™¡À»√Õ¨—ß√«¿ÌΩ‚’‚¥ŒªÓ∂صƒ÷ÿ“™–‘£¨–£—ß…˙ª·‘⁄ƒ≥ÃÏŒÁ≤Õ∫Û£¨Àʪ˙µ˜≤È¡À≤ø∑÷Õ¨—ß’‚≤Õ∑π≤Àµƒ £”ý«Èøˆ£¨≤¢Ω´Ω·π˚Õ≥º∆∫ÛªÊ÷∆≥…¡À»ÁÕºÀ˘ 浃≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ


£®1£©’‚¥Œ±ªµ˜≤ȵƒÕ¨—ßπ≤”–_______√˚£ª
£®2£©∞—Ãı–ŒÕº≤π≥‰ÕÍ’˚£ª
£®3£©–£—ß…˙ª·Õ®π˝ ˝æð∑÷Œˆ£¨π¿º∆’‚¥Œ±ªµ˜≤ȵƒÀ˘”–—ß…˙“ª≤Õ¿À∑—µƒ ≥ŒÔø…“‘π©15√˚≥…ƒÍ»À”√“ª≤Õ£Ææð¥Àπ¿À„£¨∏√–£1800√˚—ß…˙“ª≤Õ¿À∑—µƒ ≥ŒÔø…π©∂ý…Ÿ≥…ƒÍ»À ≥”√“ª≤Õ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“þ«È±¨∑¢£¨ƒ≥∆Û“µ◊º±∏◊™–Õ…˙≤˙ø⁄’÷£Æ∏√∆Û“µ‘⁄ –≥°…œŒÔ…´µΩ¡Ω÷÷…˙≤˙![]() ø⁄’÷µƒ…˱∏£¨»Ù≤…π∫2î
ø⁄’÷µƒ…˱∏£¨»Ù≤…π∫2î![]() –Յ˱∏£¨5î
–Յ˱∏£¨5î![]() –Յ˱∏‘Úπ≤–Ë“™430ÕÚ‘™£ª»Ù≤…π∫5î
–Յ˱∏‘Úπ≤–Ë“™430ÕÚ‘™£ª»Ù≤…π∫5î![]() –Յ˱∏£¨2î
–Յ˱∏£¨2î![]() –Յ˱∏‘Úπ≤–Ë“™550ÕÚ‘™£Æ“—÷™
–Յ˱∏‘Úπ≤–Ë“™550ÕÚ‘™£Æ“—÷™![]() –Յ˱∏√øî√øÃÏø…“‘…˙≤˙19ÕÚ∆¨
–Յ˱∏√øî√øÃÏø…“‘…˙≤˙19ÕÚ∆¨![]() ø⁄’÷£ª
ø⁄’÷£ª![]() –Յ˱∏√øî√øÃÏø…“‘…˙≤˙8ÕÚ∆¨
–Յ˱∏√øî√øÃÏø…“‘…˙≤˙8ÕÚ∆¨![]() ø⁄’÷£Æ
ø⁄’÷£Æ
£®1£©«Û![]() °¢
°¢![]() ¡Ω–Յ˱∏µƒ≤…π∫µ•º€∑÷± «∂ý…ŸÕÚ‘™/î£ø
¡Ω–Յ˱∏µƒ≤…π∫µ•º€∑÷± «∂ý…ŸÕÚ‘™/î£ø
£®2£©∏√∆Û“µ◊º±∏≤…π∫![]() °¢
°¢![]() ¡Ω–Յ˱∏π≤10µ´ƒÐ”√¿¥≤…π∫…˱∏µƒ◊ Ω≤ª≥¨π˝700ÕÚ‘™£¨ƒ«√¥»Á∫Œ∞≤≈≈≤…π∫∑Ω∞∏£¨”√’‚–©…˱∏√øÃÏ…˙≤˙µƒ
¡Ω–Յ˱∏π≤10µ´ƒÐ”√¿¥≤…π∫…˱∏µƒ◊ Ω≤ª≥¨π˝700ÕÚ‘™£¨ƒ«√¥»Á∫Œ∞≤≈≈≤…π∫∑Ω∞∏£¨”√’‚–©…˱∏√øÃÏ…˙≤˙µƒ![]() ø⁄’÷◊Ó∂ý£ø√øÃÏ◊Ó∂ýø……˙≤˙∂ý…ŸÕÚ∆¨
ø⁄’÷◊Ó∂ý£ø√øÃÏ◊Ó∂ýø……˙≤˙∂ý…ŸÕÚ∆¨![]() ø⁄’÷£ø
ø⁄’÷£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() «
«![]() µƒƒ⁄Ω”’˝ Ʊþ–Œµƒ“ª±þ£¨
µƒƒ⁄Ω”’˝ Ʊþ–Œµƒ“ª±þ£¨![]() ∆Ω∑÷
∆Ω∑÷![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨‘Úœ¬¡–Ω·¬€’˝»∑µƒ”–£® £©
£¨‘Úœ¬¡–Ω·¬€’˝»∑µƒ”–£® £©
¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() £ª¢Ð
£ª¢Ð![]() £Æ
£Æ

A. 1∏ˆ B. 2∏ˆ C. 3∏ˆ D. 4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
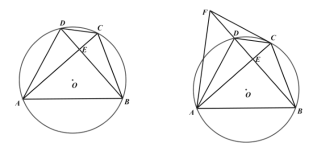
°æƒø°øÀƒ±þ–Œ![]() «
«![]() µƒƒ⁄Ω”Àƒ±þ–Œ£¨
µƒƒ⁄Ω”Àƒ±þ–Œ£¨![]() £¨
£¨![]() £¨¥π◊„Œ™
£¨¥π◊„Œ™![]() £Æ
£Æ
£®1£©»ÁÕº1£¨«Û÷§£∫![]() £ª
£ª
£®2£©»ÁÕº2£¨µ„![]() ‘⁄
‘⁄![]() µƒ—”≥§œþ…œ£¨«“
µƒ—”≥§œþ…œ£¨«“![]() £¨¡¨Ω”
£¨¡¨Ω”![]() °¢
°¢![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
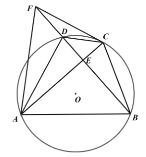
£®3£©»ÁÕº3£¨‘⁄£®2£©µƒÃıº˛œ¬£¨»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡œ¬√ʵƒ≤ƒ¡œ£∫
»Áπ˚∫Ø ˝ y£Ωf£®x£©¬˙◊„£∫∂‘”⁄◊‘±‰¡ø x µƒ»°÷µ∑∂Œßƒ⁄µƒ»Œ“‚ x1£¨x2£¨
£®1£©»Ù x1£ºx2£¨∂º”– f£®x1£©£ºf£®x2£©£¨‘Ú≥∆ f£®x£© «‘ˆ∫Ø ˝£ª
£®2£©»Ù x1£ºx2£¨∂º”– f£®x1£©£æf£®x2£©£¨‘Ú≥∆ f£®x£© «ºı∫Ø ˝£Æ
¿˝Ã‚£∫÷§√˜∫Ø ˝f£®x£©£Ω![]() £®x£æ0£© «ºı∫Ø ˝£Æ
£®x£æ0£© «ºı∫Ø ˝£Æ
÷§√˜£∫…Ë 0£ºx1£ºx2£¨
f£®x1£©©Åf£®x2£©£Ω![]() £Æ
£Æ
°þ0£ºx1£ºx2£¨
°ýx2©Åx1£æ0£¨x1x2£æ0£Æ
°ý![]() £æ0£Æº¥ f£®x1£©©Åf£®x2£©£æ0£Æ
£æ0£Æº¥ f£®x1£©©Åf£®x2£©£æ0£Æ
°ýf£®x1£©£æf£®x2£©£Æ
°ý∫Ø ˝ f£®x£©=![]() £®x£æ0£© «ºı∫Ø ˝£Æ
£®x£æ0£© «ºı∫Ø ˝£Æ
∏˘æð“‘…œ≤ƒ¡œ£¨Ω‚¥œ¬√ʵƒŒ £∫
“—÷™∫Ø ˝![]() £Æ
£Æ
f£®©Å1£©£Ω![]() +£®©Å2£©£Ω-1£¨f£®©Å2£©£Ω
+£®©Å2£©£Ω-1£¨f£®©Å2£©£Ω![]() +£®©Å4£©£Ω
+£®©Å4£©£Ω![]() £Æ
£Æ
£®1£©º∆À„£∫f£®©Å3£©£Ω £¨f£®©Å4£©£Ω £ª
£®2£©≤¬œÎ£∫∫Ø ˝![]() « ∫Ø ˝£®ÃÓ°∞‘ˆ°±ªÚ°∞ºı°±£©£ª
« ∫Ø ˝£®ÃÓ°∞‘ˆ°±ªÚ°∞ºı°±£©£ª
£®3£©«Î∑¬’’¿˝Ã‚÷§√˜ƒ„µƒ≤¬œÎ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com