
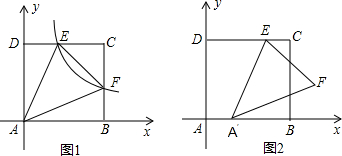
���� ��1�����ݷ���������ͼ���ϵ�������ص�ɵó�DE=BF���ʿɵó����ۣ�
��2����DE=BF=a����CE=4-a��CF=4-a������S��AEF=S������ABCD-S��ADE-S��ABF-S��ECF���ɵó�a��ֵ�������ɵó������������Ľ���ʽ��
��3�����ݣ�2����EF�����������t��ʾ��AB��BG��CE=CK�ij����ٷ�0��t��2��2��t��4��������������ۣ�
��� ��1��֤�����ߵ�E��F���ڷ���������y=$\frac{k}{x}$��k��0����ͼ���ϣ�
��AD•DE=AB•BF��
��AD=AB��
��DE=BF��
�ڡ�ADE���ABF�У�
$\left\{\begin{array}{l}AD=AB\\��ADE=��ABF\\ DE=BF\end{array}\right.$��
���ADE�ա�ABF��
��AE=AF��
��2���⣺��DE=BF=a����CE=4-a��CF=4-a��
�ߡ�AEF�����Ϊ6��
��S��AEF=S������ABCD-S��ADE-S��ABF-S��ECF
=4��4-$\frac{1}{2}$��4a-$\frac{1}{2}$��4a-$\frac{1}{2}$��4-a����4-a��
=16-4a-$\frac{1}{2}$��4-a����4-a��
=6��
���a=2��
��EF=2��4=8��
�෴���������Ľ���ʽΪy=$\frac{8}{x}$��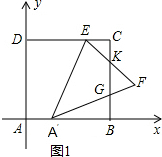
��3���⣺��0��t��2ʱ����ͼ1��ʾ��
���ɣ�2��֪E��2��4����F��4��2����
��A��B=4-t��BG=$\frac{1}{2}$AB=2-$\frac{1}{2}$t��CE=CK=2-t��
��S=S������ABCD-S������AA��ED-S��ABG-S��ECK
=4��4-$\frac{1}{2}$����2+t+t����4-$\frac{1}{2}$��4-t��•��2-$\frac{1}{2}$t��-$\frac{1}{2}$��2-t����2-t��
=16-4-4t-$\frac{1}{4}$t2-4+2t-2-$\frac{1}{2}$t2+2t
=-$\frac{3}{4}$t2+6��
��2��t��4ʱ����ͼ2��ʾ��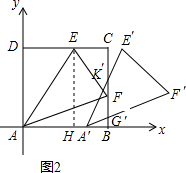
����E��EH��x���ڵ�H����EH=4��AH=2��BF=2��AB=4��
�ߡ�AEF��ÿ��1����λ���ٶ���x���������ƽ�ƣ�
��AE��A��E�䣬AF��A��B�䣬
��$\frac{EH}{AH}$=$\frac{K��B}{A��B}$����$\frac{4}{2}$=$\frac{K��B}{4-t}$�����K��B=2��4-t��=8-2t��
ͬ����$\frac{BF}{AB}$=$\frac{BG��}{A��B}$����$\frac{2}{4}$=$\frac{BG��}{4-t}$�����BG��=2-$\frac{t}{2}$��
��S=S��A��G��K��=$\frac{1}{2}$G��K��•A��B=$\frac{1}{2}$��K��B-BG�䣩•A��B
=$\frac{1}{2}$��8-2t-2+$\frac{t}{2}$��•��4-t��
=$\frac{1}{2}$��6-$\frac{3}{2}$t��•��4-t��
=$\frac{3}{4}$t2-6t+12��
��S=$\left\{\begin{array}{l}-\frac{3}{4}{t}^{2}+6��0��t��2��\\ \frac{3}{4}-6t+12��2��t��4��\end{array}\right.$��
���� ���⿼����Ƿ����������ۺ��⣬�漰������������ͼ���ϵ�������ص㡢�����ε����ʼ����ε������ʽ��֪ʶ���ڽ�����ʱҪע������˼������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
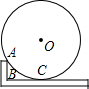 ľ��ʦ�������ýdz߲����������Բ�İ뾶����ͼ���ýdzߵĽ϶̱߽�����O�ڵ�A����ʹ�ϳ������O�����ڵ�C���ǽdzߵ�ֱ�Ƕ���ΪB������AB=8cm��BC=16cm�����O�İ뾶����20cm��
ľ��ʦ�������ýdz߲����������Բ�İ뾶����ͼ���ýdzߵĽ϶̱߽�����O�ڵ�A����ʹ�ϳ������O�����ڵ�C���ǽdzߵ�ֱ�Ƕ���ΪB������AB=8cm��BC=16cm�����O�İ뾶����20cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 47��49 | B�� | 48��49 | C�� | 47��46 | D�� | 48��46 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | -5 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����a��a��������������������Ҫ��
��֪����a��a��������������������Ҫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | 2 | C�� | -4��2 | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪ͼ1��ͼ2��ͼ3����4��5�ķ���ֽ������ÿ��С�����εı߳���Ϊ1cm��ÿ��С�����εĶ����Ϊ��㣮
��֪ͼ1��ͼ2��ͼ3����4��5�ķ���ֽ������ÿ��С�����εı߳���Ϊ1cm��ÿ��С�����εĶ����Ϊ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1080�㣬180�� | B�� | 1080�㣬360�� | C�� | 720�㣬180�� | D�� | 720�㣬360�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3•a2=a6 | B�� | ��a+b��2=a2+b2 | C�� | x5+x5=x10 | D�� | ��-ab��5�£�-ab��2=-a3b3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com